It means that if the system begin to work from some domain of initial values, than will exist domain as
![]()
with some domain
of attraction ![]() , for
which the target condition (3) fair according to a lemma [10].
, for
which the target condition (3) fair according to a lemma [10].
However preservation of domain of dissipative does not guarantee,
that in the singular-disturbing system many
attraction ![]() remain
the same.
remain
the same.
Let in (13) ![]() . Let’s will consider that movement of system begin in initial
number of entry conditions
. Let’s will consider that movement of system begin in initial
number of entry conditions ![]() , consequently all trajectories of
the system will be is in domain of dissipative
, consequently all trajectories of
the system will be is in domain of dissipative ![]() according to lemma [10].
according to lemma [10].
Let’s consider Lyapunov function as (15) again, and will take a derivative from Lypunov function on trajectories of the systems (12) and (13), taking into account the result in (16)
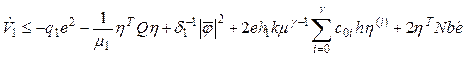 . (17)
. (17)
Take into attention correlations
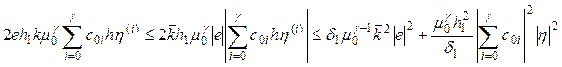 ,
,
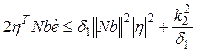 , where
, where ![]() ,
, ![]() ,
,
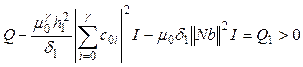 ,
, ![]() -
single matrix,
-
single matrix,
for derivative from Lyapunov function (17), will receive
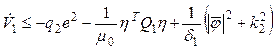 .
.
One can see that changing ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() can change the value
can change the value ![]() in the target condition
(3). And, choosing
in the target condition
(3). And, choosing ![]() as big enough, value of function
as big enough, value of function ![]() can make as such as small, that is reducing trajectories (12) to small enough neighborhood of
can make as such as small, that is reducing trajectories (12) to small enough neighborhood of ![]() .
.
3. Example
Let’s consider unstable system ![]() and reference model, which set by the following equation
and reference model, which set by the following equation ![]() , where
, where ![]() .
.
In the algorithm of estimation (9) choose such parameters as: ![]() ,
, ![]() ;
; ![]() . As
. As ![]() , then filter on an output
and an input are expelled and then vector will be formed as
, then filter on an output
and an input are expelled and then vector will be formed as ![]() . The law of control is
formed as the equation
. The law of control is
formed as the equation ![]() , and in the algorithm of adjustment (12) parameters
, and in the algorithm of adjustment (12) parameters ![]() and
and ![]() will choose as
will choose as ![]() and
and ![]() .
.
In the figure the results of modeling of transitional processes of
tracking error for reference signal ![]() and the law of control
and the law of control ![]() at the following meaning of parameters of plant (1):
at the following meaning of parameters of plant (1): ![]() . All other entry values
in the system will accept equal zero too.
. All other entry values
in the system will accept equal zero too.
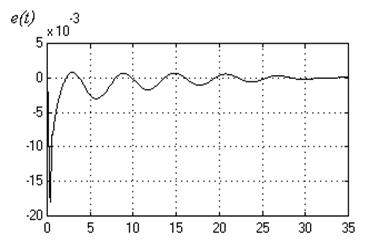
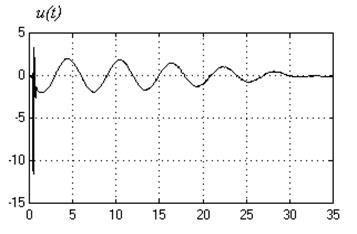
4. Conclusion
In the work for the linear plant, set in the form of an input-output with unknown parameters and with scalar input and output, which accessible to measurement, is considered the construction of adaptive law of control on the base of offered scheme of parameterization of control plant (1), resulting to SPR-function and on the base of modified algorithm of adaptation. In the tie of what filters through which all components of vector are passed, are expelled. The offered approach allows to simplify the construction of the closed control system and to reduce the order of closed-loop system. It gives concerning small algorithm. Modeling on the computer shows good results, both, on tracking error and on control influence.
5. REFERENCES
[1] V. O. Nikiforov, and A. L. Fradkov, “The scheme of adaptive control with an extended error signal”, Avtomatika i telemekhanika, no. 9, 1994, pp. 3-22 (in Russian).
[2] A.S. Morse, A. Isidori, “High-order parameter tuners for adaptive control on nonlinear system”, Tarn T. I. (eds). Systems, Models and Feedback: Theory and Applications. Birkhanser, 1992, pp. 339-364.
[3] V.O. Nikiforov, “Robust high-order tuner of simplified structure”, Automatica, vol. 35, no 8, 1999, pp. 1409-1417.
[4] I. V. Miroshnik, V. O. Nikiforov, and A. L. Fradkov, Nonlinear and adaptive control of complex Dynamical systems, St. - Petersburg: Nauka, 2000 (in Russian).
[5] A. Feuer, and A.S. Morse, “Adaptive control of single input, single-output linear systems”, IEEE Trans. on Automat. Control, vol. 45, no. 3, 2000, pp. 490-494.
[6] H.K. Khalil, “Universal integral controllers for minimum-phase nonlinear systems”, IEEE Trans. on Automat. Control, vol. 45, no. 3, 2000, pp. 490-494.
[7] H.K. Khalil, “Adaptive output feedback control of nonlinear systems represented by input-output models”, IEEE Trans. On Automatic Control, vol. 41, no. 2, 1996, pp. 177-188.
[8] N.A. Mahmoud, and H.K. Khalil, “Robust control for a nonlinear servomechanism problem”, Int. J. Control, vol. 66, no. 6, 1997, pp. 779-802.
[9] A.L. Fradkov, “Synthesis of adaptive system of stabilization of linear dynamic plants”, Avtomatika i telemekhanika, no.12, 1974, pp. 96-103 (in Russian).
[10] V.A. Brusin, “About one class of singular-disturbing adaptive systems. 1”, Avtomatika i telemekhanika, no.4, 1995, pp. 119-127 (in Russian).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.