, (5)
where 
and accordingly 
. Then, with the account
of equation of reference model (2) and parametrical equation of plant (4), will
make expression for an error of following 
as
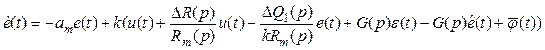, (6)
where 
- an estimation of an
error 
, and it will be
formed lower; 
is
function of deviation; 
is bounded function of time in the force Hurwitz of polynomial 
and assumption A2 and A4.
And on the base of the equation (6) will form the state filters
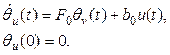(7)
Here 
; 
- a numbering matrix in
the Frobenius form with characteristic polynomial ; 
. Then vector for the
equation (6) and filters (7) will form as a vector 
. If to set the law of
control as 
,
where 
- vector of
adjusted parameters, than the equation (6) can be rewrite as
, (8)
where 
- vector of unknown
parameters, depending on coefficients of polynomials 
, 
and 
.
As the possibility of measuring of derivative of an output of
control plant (1) and reference model (2) is absent, so for realization of
evaluation 
-
derivative of function can use any of observers [for example, 6-8]. Let’s make use of
scheme, which offered in [7, 8].
, 
, (9)
where 
; 
, 
- single matrix of order 
; 
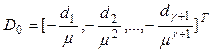, where 
are chosen from the condition of stable of matrix 
, where 
; 
; 
- small enough value. In these case in the law of control variables from the observer
(9) will be used, it means that in conditions of measuring only
, the law of control is
technical realized. How it will be shown lower, for realization of the
closed-loop control system the order of observer (9) can be chosen equal , but for the proof the
order of observer is used equal 
to estimate - derivatives of function .
So, let’s enter into consideration vector of deviation 
, where 
, 
. Having taken the
derivative from vector of deviation 
on time, will receive 
. The equation of deviation what in the force of equation (9) and
vector of deviation will be as 
. Let’s transform the equation of deviation and vector of deviation
to the equivalent equation relative an output 
, 
. (10)
Where 
. On the base of equations
(9) and (10) rewrite the equation (8) as
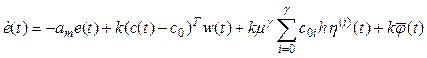, (11)
where 
- unknown constant coefficients, and depend on coefficients of
polynomial .
Statement.
If 
is SPR-function, than there is a number 
and algorithm of
adaptation
, (12)
such that if 
, 
and 
, than the system of
control (7), (8), (9) and (12) dissipative, if movement of the system begins in
some domain 
and
target condition (3) is fulfilled, where - domain, and determined by the entry conditions of plant (1).
Proof. Let’s write down the equations (10) and (11) as
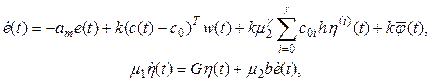(13)
where 
. Use with a lemma [10].
Lemma [10]. If the system is described
by the equation 
, 
, 
, where 
- an continuous Lipshec function on 
and if 
has the bounded closed
domain of dissipative 
, where 
- undermined piece-smooth
positively determined function in 
will exist 
such that if 
than the initial system has domain of dissipative 
, when for some numbers 
and 
when 
is fulfilled condition
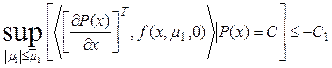, (14)
when 
.
Let's take Lypunov function for equation (13) as
,
where 
; matrix 
is determined from the
equation 
, 
. Then, having taken a
derivative on time when will receive
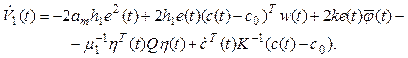(15)
Having used with identity 
, with estimations 
, 
, 
, 
and with equation (12),
will receive
. (16)
From fulfillment of inequality (16) follows the boundedness of
functions , and 
. As 
is bounded, so from (13)
quantities 
, 
and 
are bounded too. Function
will be bounded
in the force of Hurwitz of matrix and boundedness . As the vector-function - bounded, than -derivatives of signal 
also will be bounded in the force of ways of formation of the vector
. Function 
according to the
assumption A3, is also the bounded function. Further, will transform the second
equation (7)
,
from where
follows the boundedness 
, because 
, matrix 
has a characteristic polynomial 
, which according to the assumption A2 is Hurwitz. So vector 
is bounded. As , and 
is bounded vector in the
force of boundedness , than controlling influence is bounded function too.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.