Pattern recognition control by synergetic computer

 PATTERN RECOGNITION CONTROL

BY SYNERGETIC COMPUTER

Kirill V. Nikitin, Sophya V. Zhukova

Department of Technical Cybernetics

Saint-Petersburg State Polytechnic University

29 Polytechnicheskaya st., Saint-Petersburg, 195251, RUSSIA

Tel: +7(812) 3434459, E-mail: drezet@gmail.com, flyingbug2@mail.ru

Abstract – pattern recognition problem with use of Synergetic Neural Network – Synergetic Computer is considered in this paper. This network capabilities in pattern recognition control are demonstrated. The problem of human faces recognition is solved.

1. INTRODUCTION

One of the key problems in control theory at the present time is intellectual systems creating, which are able to control an object with non-formalizable functioning in complex environment.

In such systems every situation is considered as a separate pattern, that have to be processed to form a control action decision. So the main problem to be solved by intelligence system is problem of associative memory or pattern recognition.

Pattern recognition is one of non-trivial tasks, performed by human brain. Formally pattern recognition is defined as classifying process, where input signal/pattern is being related to one of predetermined classes. The solution of pattern recognition problem may be found in more detailed and realistic reconstruction of recognition process, performed by brain. Functional algorithmization solution is characterized by exponential complexity growth when problem dimension increases. Another way is to use neural networks paradigm. All the more neural networks are similar to some parts of brain cortex by construction and properties.

As pattern recognition is dynamical process, it is better to use recurrent neural networks, characterized by complex behavior and dynamics. The most common approach to pattern recognition, based on recurrent neural networks is control of their multidimensional dynamics or using the subset of separate steady states – attractors. Each pattern is brought in correspondence with an attractor. After initializing neural network with input pattern, its dynamic finally converges network state to the attractor, which represents stored pattern.

One of the first attractor neural networks model is Hopfield network, which have physical structure similar to spin glasses. Hopfield model, however, have a number of disadvantages such as storing of false patterns, small memory capacity and long recognition time. H. Haken proposed a model of synergetic neural network [1], which is also an attractor neural network, but has more complex structure in comparison with Hopfield network. Main  features of synergetic neural network are absence of false patterns and the fact that its functioning can be described by order parameter dynamics. The order parameters characterize stored patterns. This possibility allows easy pattern recognition controlling, in particular recognition system attention controlling.

2.  SYNERGETIC COMPUTER DESCRIPTION

2.1. Mathematical model of synergetic computer

In the synergetic neural network, just as in Hopfield model, during pattern recognition system converges to the state with minimal energy. In Haken model all minimums are definitely corresponded to stored patterns. And this is a great advantage over Hopfield model, where minimums are corresponded not only to stored but also to false patterns.

Assume that the system state is given with vector , where N – is a number of elements or system components. Then equation, describing the process of recognition in synergetic computer is given by 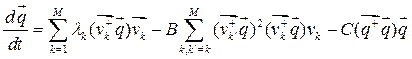[1]:

,                                                                   (1)

where M is a number of stored patterns, are vectors, representing stored patterns and  are vectors, adjacent to vectors of stored patterns.

First item in (1) contains attention parameters . Stored pattern can be recognized only if corresponding attention parameter is positive. Value of this parameters set borders to domains of attraction.

Any initial state vector , belonging to domain of attraction of kth  pattern, finally converges to the attractor, which corresponds to stored pattern .

System movement to the attractor can be defined with use of energy function [1]:

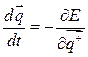                                                                                                                                                     (2)

Using (2), we can get general expression for current energy state of the synergetic computer [1]:

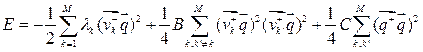                                                                 (3)

First item in (3) plays dominant role in the equilibrium point neighborhood. Energy state descriptions of Hopfield model and many other known models are limited by this item [2].

Equations (1)-(3) describe micro-level dynamics in the system state space.  The transition to macro-level can be done using decomposition of vector  to vectors  of stored patterns [1]: