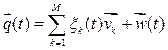Pattern recognition control by synergetic computer, страница 2

,                                                                                                                                (4)

where  is order parameter, belonging to vector-pattern  and  is remainder component which converges with time to zero. So system state evolution can be fully defined with order parameters .  Substituting equation (4) in (1) one can get equation, describing recognition process on the level of order parameters:

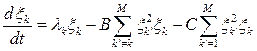                                                                                                           (5)

Initial values for order parameters can be defined in the following way [1]:

                                                                                                                                         (6)

So, equations (4)-(6) describe macro-level dynamics on the order parameters level.

2.2. Architecture of the synergetic computer

Synergetic computer can be realized in two ways. So there can be used two different architectures of synergetic neural network.

First method is based on using  equation (1). This method is natural, because it describes system behavior on the state level with all inherent particular qualities. To use equation (1) in this method it has to be transformed to form with explicitly expressed components  of system state vector:

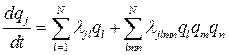                                                                                                                  (7)

Comparing (1) and (7) one can find all coefficients  , and, so, calculate all neural network weight coefficients. According to this method architecture of synergetic computer is presented on figure 1. Every neuron there functions according to equation (7).

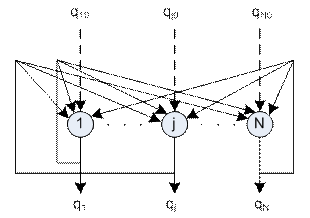
Figure 1. First method of synergetic computer building

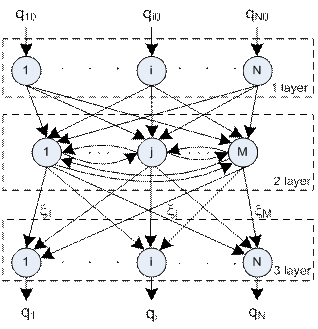
Figure 2. Second method of synergetic computer building

Second method of building synergetic computer is based on using the order parameter paradigm. Architecture of network for this case is presented on figure 2.

It is third-layer network. First layer receives input patterns.  Second layer represents order parameters, corresponding to stored patterns. First layer output signal sets initial values of second layer order parameters. Strength of connections between first and second layers is defined by eq. (6)

Layer of order parameters has concurrent dynamics, defined by eq. (5). While this layer works one of order parameters wins and its value becomes 1, though all other order parameters converge to zero. The won order parameter excites neurons of the third layer, and on the third layer output  appears stored pattern, corresponding to this won order parameter. Connection strengths between the layers in this case are defined by eq. (4) without taking into account error w.

2.3. Synergetic computer learning

Synergetic computer learning is finding neural networks weight coefficients, which in their turn are defined through the vectors of stored patterns , adjacent to them vectors  and attention parameters . Therefore, synergetic computer learning procedure consists of finding vectors  and setting attention parameters .

To solve this task there exist two methods according to demands and conditions.

If it is assumed that vectors of stored patterns are well known and their total number allows sufficiently quickly to calculate adjacent to them vectors, then it is rational to evaluate adjacent vectors  by known vectors  using known algorithms. Disadvantage of this method is low efficiency when storing new pattern in system.

Second method was suggested in [3] and by its properties it appears to be optimization. Its application is appropriate when data about stored pattern is inexact and is changing in time. Unknown vectors are found using minimization of functional (5) relative to variables . On the network input learning signal in the form of vector  is given. Simultaneously optimal values of , minimizing (5) are looked for. In view of functional properties unknown vectors can be found. Attention parameters can be used to control learning process, setting for example which vectors corresponds to new patterns.

3. EXPERIMENTAL RESULTS

3.1. Description of experimental environment

To investigate control pattern recognition by synergetic computer there was written a program in Matlab 6.5 programming environment. In this program two architectures of synergetic computer (fig.1,2) were realized on modeling level. All of the patterns in program are set as two-dimensional image, consisting of set of pixels. Pixels are coded with 8 bits and can be represented through 256 shades of gray color.

Each of patterns at first comes through the preprocessing for satisfying necessary conditions [1]:

·  two-dimensional feature (pixel value) array transforms to one-dimensional;