|
Работа |
tрнij |
tij |
tроij |
tпнij |
tij |
tпоij |
Rпij |
|
|
|
i |
j |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
5. Анализ и оптимизация сетевой модели
На этом этапе выполняется анализ созданной модели и принимаются меры для ее оптимизации. Вопрос о необходимости оптимизации сетевой модели по времени решается в зависимости от знамения вероятности выполнения завершающего события (Рк) в директивный срок.
Для определения знамения вероятности Рк рассчитывают:
1. дисперсию продолжительности работ, лежащих на критическом пути
![]() (см. табл. 1)
(см. табл. 1)
2. значение аргумента функции нормального распределения вероятностей
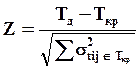 , где Тд - заданный директивный срок
выполнения разработки;
, где Тд - заданный директивный срок
выполнения разработки;
3. по значению аргумента Z в таблице 2 находится значение вероятности Рк.
Если значение Рк лежит в пределах 0,35 - 0,65, то можно считать, что разработка уложится в директивный срок.
Если значение Рк выходит за пределы указанных границ - сетевая модель требует оптимизации.
При выходе значения Рк за левую границу оптимизация должна быть направлена на сокращение длительности критического пути.
Сократить продолжительность критического пути можно следующим образом:
1. изменением топологии модели с целью замены последовательного выполнения работ параллельным там, где это допускается характером технологии и организационных условий выполнения работ;
2. перераспределением ресурсов между работами сетевой модели, состоящим в том, что часть ресурсов (рабочая сила, оборудование, финансовые средства и т.п.) снимается с работ, не принадлежащих критическому пути и имеющих большие резервы времени, и распределяется на работы критического пути, сокращая их продолжительность;
3. ужесточением оценок продолжительностей работ.
Выход значения Рк за правую границу означает избыток резервов времени выполнения работ и возможность сокращения их продолжительности.
Значения функции Рк
|
Z |
Рк |
Z |
Рк |
Z |
Рк |
|
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 |
0,5000 0,5398 0,5793 0,6179 0,6554 0,6915 0,7257 0,7580 0,7881 0,8159 0,8413 0,8643 0,8849 0,9032 0,9192 0,9332 0,9452 0,9554 0,9641 0,9713 0,9772 |
2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 -3,0 -2,9 -2,8 -2,7 -2,6 -2,5 -2,4 -2,3 -2,2 -2,1 -2,0 |
0,9821 0,9861 0,9893 0,9918 0,9938 0,9953 0,9965 0,9974 0,9981 0,9987 0,0013 0,0019 0,0026 0,0035 0,0047 0,0062 0,0082 0,0107 0,0139 0,0179 0,0228 |
-1,9 -1,8 -1,7 -1,6 -1,5 -1,4 -1,3 -1,2 -1 -1,0 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0,0 |
0,0287 0,0359 0,0446 0,0548 0,0668 0,0898 0,0968 0,1151 0,1357 0,1587 0,1841 0,2119 0,2420 0,2743 0,3085 0,3446 0,3821 0,4207 0,4602 0,5000 |
6. Построение календарного графика распределения работ
Календарное распределение работ решает следующие задачи:
1. определение календарных сроков выполнения работ для контроля их соблюдения;
2. выявление календарного распределения загрузки персонала во времени и выравнивание ее за счет варьирования сроками выполнения работ, лежащих на ненапряженных путях.
Решение первой задачи осуществляется путем построения календарного графика, возможный вариант которого приводится в форме 2. На графике двойными линиями показаны работы, лежащие на критическом пути. Все остальные пути (ненапряженные) показаны по обе стороны от критического. Над линией работы указывается количество дней или недель, соответствующих ожидаемой продолжительности ее выполнения. Под линией работы в кодированном виде приводится перечень участвующих в ней исполнителей. Код имеет двойственную расшифровку: место в коде определяет профессию исполнителя, значение кода - количество исполнителей данной профессии. Наиболее распространенное построение кода имеет следующий вид: на первом месте слева направо - конструкторы, на втором - технологи, на третьем - исследователи, на четвертом - рабочие. Например, код 1213 расшифровывается так: один конструктор; два технолога; один исследователь; трое рабочих.
Рассмотрим пример построения календарного графика (см. форму 2). Критический путь, вытянутый в прямую линию, занимает 15 недель. Заметим, что на одни и те же события опираются части ненапряженных и критических путей, которые имеют различную продолжительность. Так, на события 3 и 8 опирается участок критического пути 3, 4, 8 и участок ненапряженного пути 3, 5, 8. Суммарная продолжительность работ (3, 5) и (5, 8) меньше продолжительности работ (3, 4) и (4, 8). Поэтому на ненапряженном пути имеется резерв времени. Часть календарного периода, в течение которого выполняется работа, показывается сплошной линией, остальное время, т.е. резерв показывается штриховой линией (см. работу 5, 8).
В соответствии с установленными календарными сроками выполнения работ должна определяться и, если необходимо, выравниваться загрузка всех исполнителей, однако в рамках одной темы (разработки) получить полную загрузку всего персонала невозможно. Поэтому в данной работе загрузка исполнителей не рассчитывается.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.