Фазовые портреты нелинейных систем и особенности нелинейной динамики

Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики

Кафедра Систем Управления и Информатики

Лабораторная работа №2

«Фазовые портреты нелинейных систем и особенности нелинейной динамики»

                                                                                            Выполнил:   Годгильдиев А,

Пронин В.

                                                                                                                          группа 4145

                                                                                        Проверил:    Пыркин А.А

Санкт-Петербург

2008

Цель работы: Исследовать системы 2-го порядка, содержащие объект управления

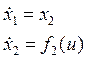
и линейный регулятор  , где  - коэффициенты обратных связей.

1.

Характеристический полином:

а) Корни характеристического полинома:

 

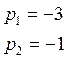
Система принимает вид:

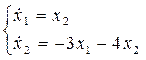
Фазовый портрет:

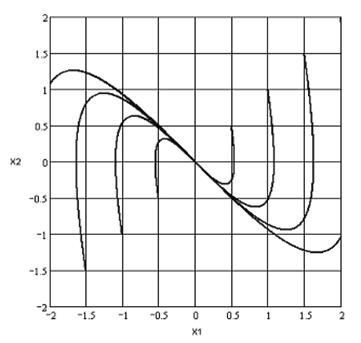
Положение равновесия: (0;0)

Асимптотическая устойчивость; тип переходного процесса – колебательный.

б) Корни характеристического полинома:

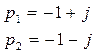
Система принимает вид:

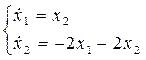
Фазовый портрет:

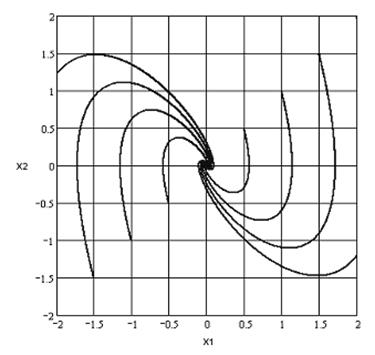
Положение равновесия: (0;0)

Асимптотическая устойчивость; тип переходного процесса – колебательный.

в) Корни характеристического полинома:

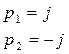
Система принимает вид:

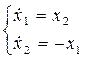
Фазовый портрет:

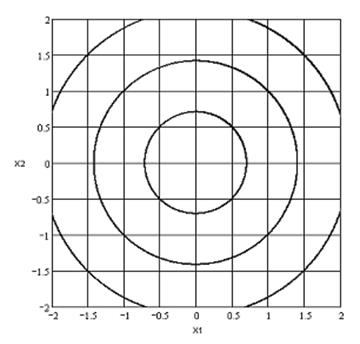
Положение равновесия: (0;0)

Устойчива по Ляпунову; тип переходного процесса – незатухающий.

2. Исследовать две гладкие нелинейные системы, для которых

а)

1) Корни характеристического полинома:

 

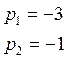
Система принимает вид:

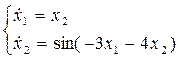
Фазовый портрет:

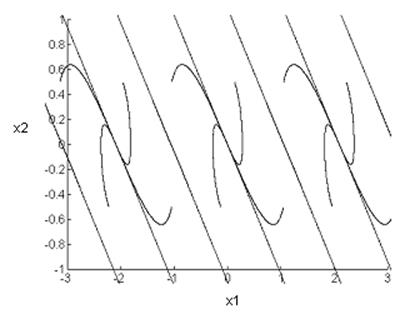
Векторное поле:

Положения равновесия:  , к – целое.

Вид переходного процесса – апериодический, затухающий, соответствует асимптотически устойчивой системе.

 - точечные аттракторы, образующие инвариантное множество.

2) Корни характеристического полинома:

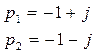
Система принимает вид:

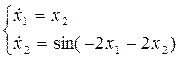
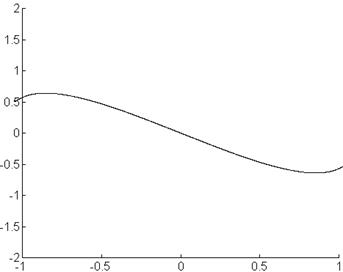
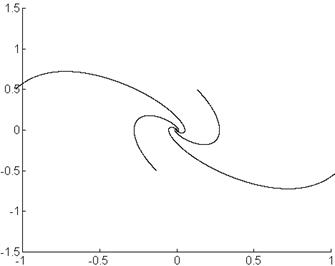
Фазовый портрет:

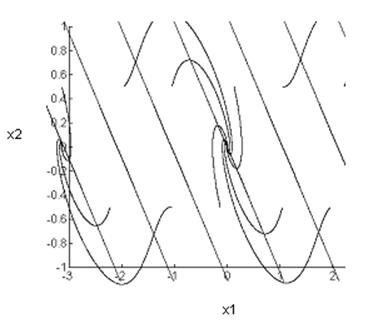
Векторное поле:

Положения равновесия: , к – целое.

Вид переходного процесса – колебательный, затухающий, соответствует асимптотически устойчивой системе.

 - точечные аттракторы, образующие инвариантное множество.

3) Корни характеристического полинома:

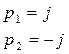
Система принимает вид:

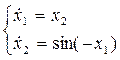
Фазовый портрет:

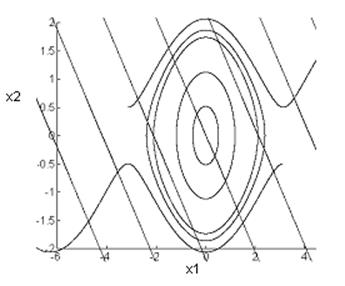
Векторное поле:

Положения равновесия: , к – целое.

Вид переходного процесса – колебательный, незатухающий, соответствует системе на колебательной границе устойчивости.

б)

1) Корни характеристического полинома:

 

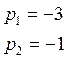
Система принимает вид:

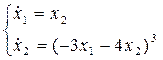
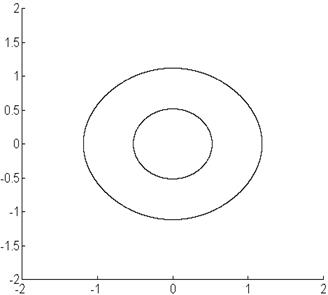
Фазовый портрет:

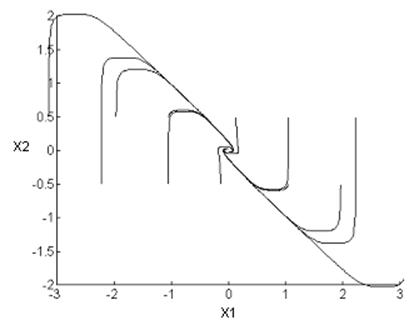
Векторное поле:

Положение равновесия: .

Вид переходного процесса – апериодический, затухающий, соответствует асимптотически устойчивой системе.

Аттракторами являются точка  и вся область .

2) Корни характеристического полинома:

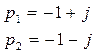
Система принимает вид:

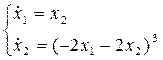
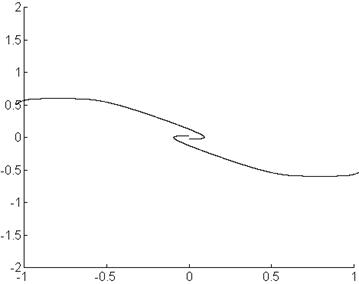
Фазовый портрет:

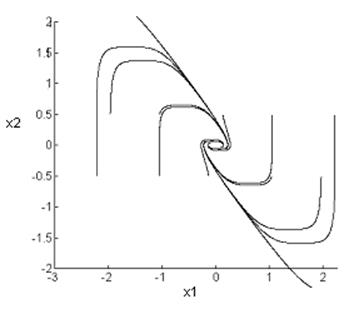
Векторное поле:

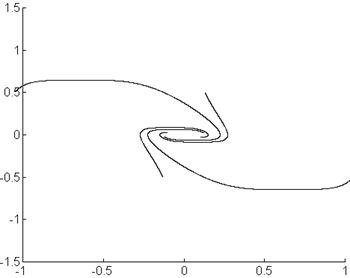
Положение равновесия: .

Вид переходного процесса – колебательный, затухающий, соответствует асимптотически устойчивой системе.

Аттракторами являются точка  и вся область .

3) Корни характеристического полинома:

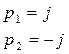
Система принимает вид:

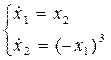
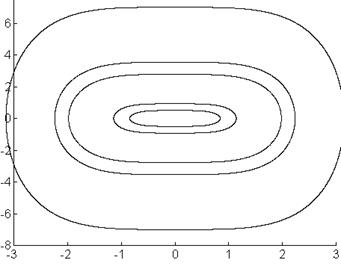
Фазовый портрет:

Векторное поле:

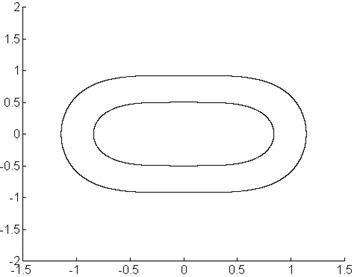
Положение равновесия: .

Вид переходного процесса – колебательный, незатухающий, соответствует системе на колебательной границе устойчивости.