Абсолютно устойчивые и гиперустойчивые системы

Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики

Кафедра Систем Управления и Информатики

Лабораторная работа №5

"Абсолютно устойчивые и гиперустойчивые системы"

                                                                                              Выполнил: Кузнецов Д.

                                                                                                                  Григорьев П.

                                                                                                                    группа 4147

                                                                                           Преподаватель:       Пыркин  А.А.

Санкт-Петербург

2008

Задание: исследовать абсолютно устойчивые и гиперустойчивые системы: построить переходные процессы, найти положения равновесия.

Нелинейная система состоит из линейного блока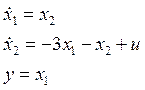

и нелинейного статического блока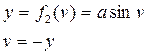

u - вход, y - выход.

Начальные условия: x₁(0) = 5, x₂(0) = 0.

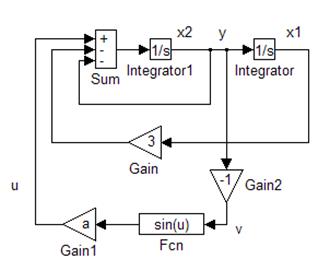
Схема моделирования системы.

Построим переходные процессы:

При a < -1 система находится на границе устойчивости колебательного типа. При a ≥ -1 система устойчива.

Найдем значения параметров k: , соответствующие границам устойчивости системы.

Таким образом, система устойчива при .

Построим графики функции , соответствующие предельно допустимым значениям параметра а.

Исходные данные:

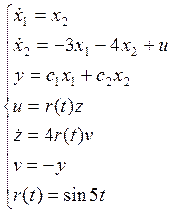
Проанализировать устойчивость системы для двух случаев:

а) ;

б)

Схема моделирования:

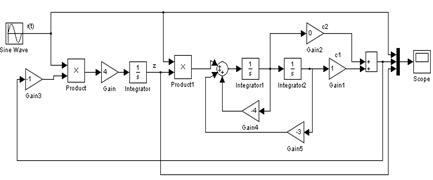
а)

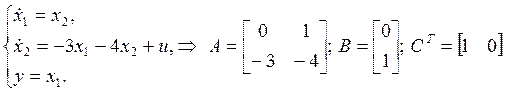
Передаточная функция находится по формуле: :

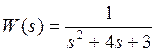
Нули передаточной функции: отсутствуют.

Полюса передаточной функции:

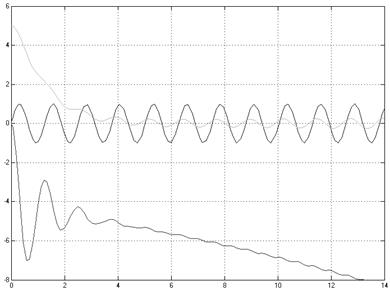
Графики переходных процессов:

Годограф :

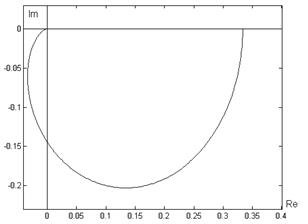
Вывод: в данном случае вход системы (нелинейный блок ) не ограничен (это видно из графика переходного процесса z(t)), а годограф передаточной функции пересекает мнимую ось, т.е. линейная часть не является строго положительной. Из этого можно сделать вывод о том, что данная система не является гиперустойчивой.

б)

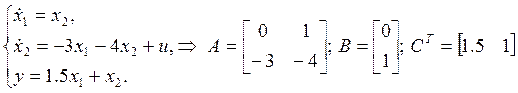
Передаточная функция:

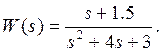
Нули передаточной функции:

Полюса передаточной функции:

Графики переходных процессов:

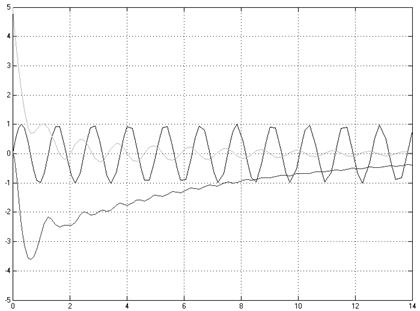
Годограф :

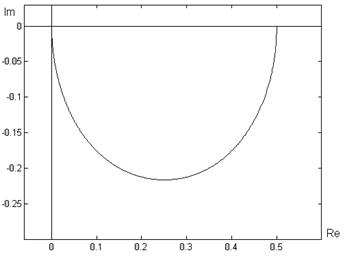
Вывод:в данном случае система, очевидно, удовлетворяет условиям для гиперустойчивой системы: линейная часть строго вещественно положительна, нелинейный блок удовлетворяет условию Попова.