Изучение простейших нелинейных систем

Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики

Кафедра Систем Управления и Информатики

Лабораторная работа №1

«Простейшие нелинейные системы»

                                                                                            Выполнили:   Годгильдиев А,

Пронин В.                                                                                                                        

группа 4145

                                                                                        Проверил:    Пыркин А.А.

Санкт-Петербург

2008

Рассмотреть нелинейные системы 1-го порядка

где  f(x)= {-x, x, -x², -x-x²,  -x ³, - sin x, -1/x, -sign x, sign x}

1. Построить функции  f(x) и  установить их класс (кусочно-непрерывные, непрерывные, гладкие), определить стационарные и сингулярные точки.

2. Построить графики переходных процессов x(t)=x(x₀,t) для различных значений начальных условий x_o.

3. Исследовать вопросы единственности и существования решений, а также полноты.

4. Определить положения равновесия систем x=x*. Оценить их  устойчивость,  найти области притяжения.

Схема моделирования:

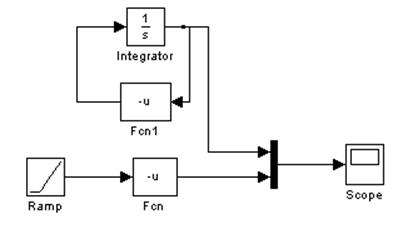
1.  f(x)=-x

1. На  функция непрерывная и гладкая.

Стационарные точки:

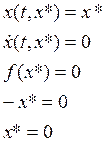
Сингулярных точек нет.

2.  Графики переходных процессов для начальных условий: х0=1,-3,-8:

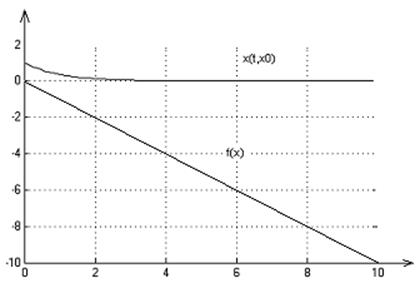
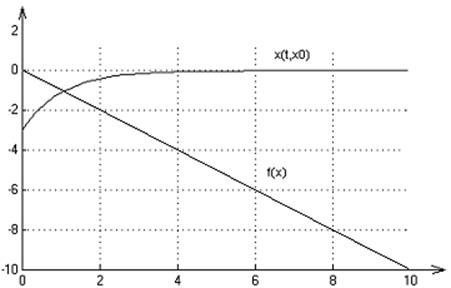
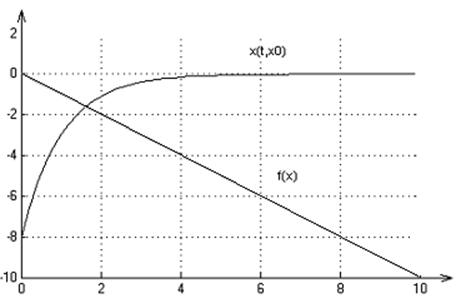
3. На множестве Х решение существует и единственно.

Система является полной, т.к. f(x) непрерывна и глобально липшицева.

4. Положение равновесия х*=0 является устойчивым с областью притяжения    .

2.  f(x)=x

1. На  функция непрерывная и гладкая.

Стационарные точки: х*=0

Сингулярных точек нет.

2.  Графики переходных процессов для начальных условий: х0=1,-4,5:

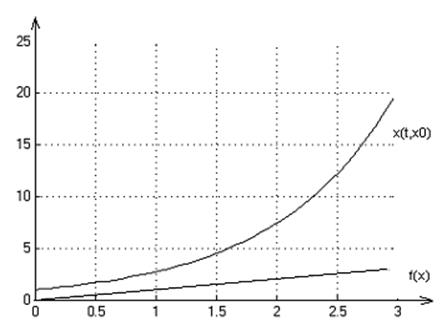
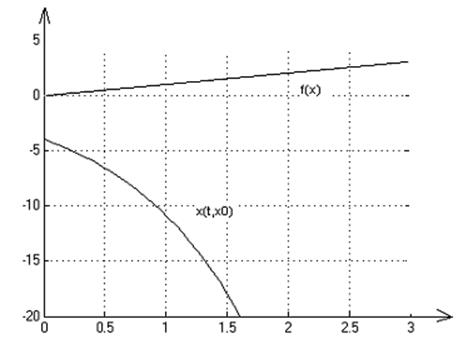
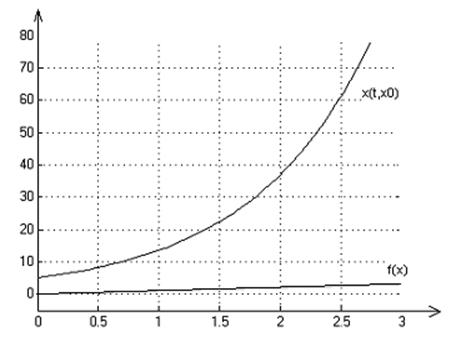
3. На множестве Х решение существует и единственно.

Система является полной, т.к. решения системы определены для любых начальных условий.

4. Положение равновесия х*=0 является неустойчивым, т.к. система не является полной ни в одной из его окрестностей.

3.

1. На  функция непрерывная и гладкая

Стационарные точки: х*=0

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=1,2,4:

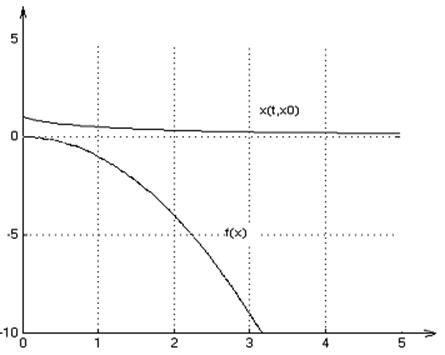
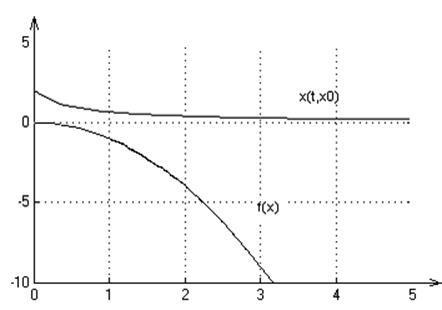
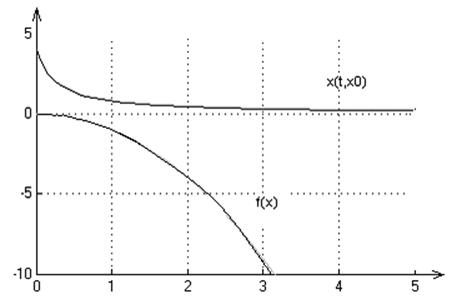
3. На множестве Х решение существует и единственно.

Система является неполной, т.к. при х0<0 решения определены только на некотором интервале времени.

4. Положение равновесия х*=0 является устойчивым с областью притяжения .

4.

1. На  функция непрерывная и гладкая

Стационарные точки: х*=0; -1.

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=1,-0.7,-1.1:

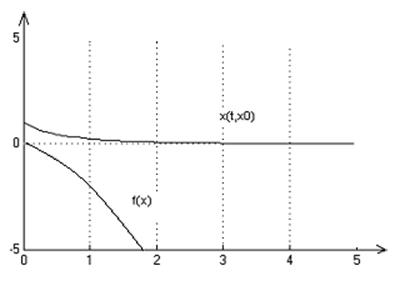
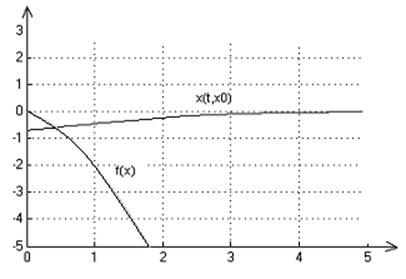
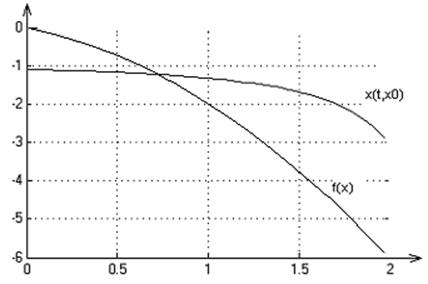
3. На множестве Х решение существует и единственно.

Система является неполной, т.к. при х0<-1 решения определены только на некотором интервале времени.

4. Положение равновесия х*=0 является устойчивым с областью притяжения .

Положение равновесия х*=-1 не является устойчивым, т.к. система не является полной ни в одной из его окрестностей.

5.

1. На  функция непрерывная и гладкая

Стационарные точки: х*=0.

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=-1,1,2:

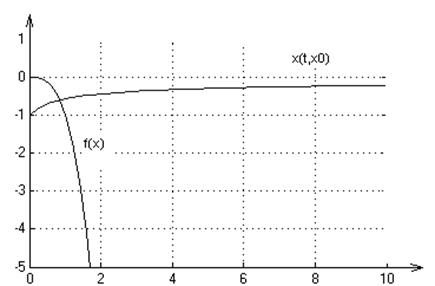
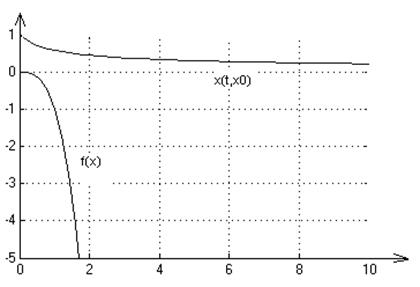
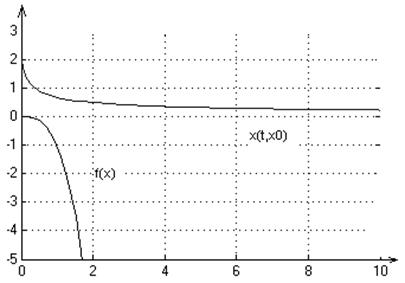
3. На множестве Х решение существует и единственно.

Система является полной, т.к. решения системы определены для любых начальных условий.

4. Положение равновесия х*=0 является устойчивым с областью притяжения .

6. f(x)=-sinx

1. На  функция непрерывная и гладкая

Стационарные точки: х*=πk,

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=-1,1,3:

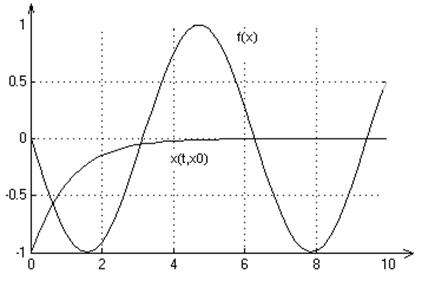
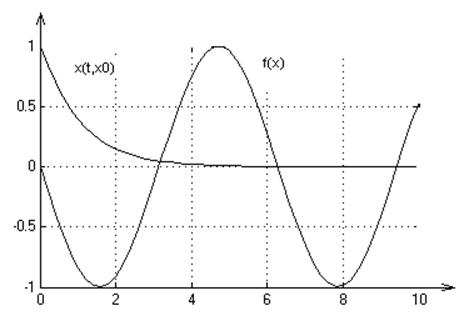
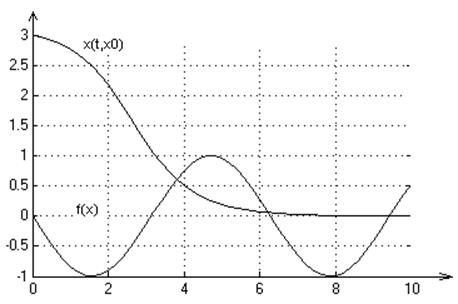
3. На множестве Х решение существует и единственно.

Система является полной, т.к. решения системы определены для любых начальных условий.

4. Положение равновесия х*= 2πk, k=...-2; -1; 0; 1; 2; 3… является устойчивым с областью притяжения .

Положение равновесия х*= (2k-1)π не является устойчивым.

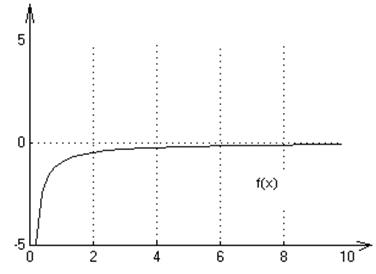
7. f(x)=-1/x

1. Функция не является непрерывной на .

Сингулярная точка х=0.

Стационарных точек нет.

2. Графики переходных процессов для начальных условий: х0=15,20:

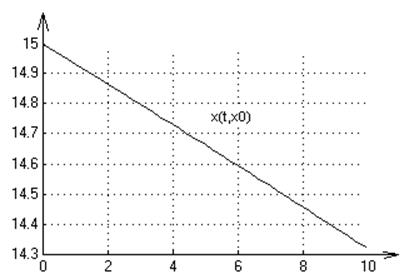
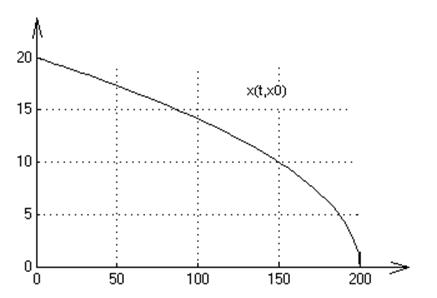
3. Для х=0 решение не существует. В противном случае решение существует и единственно.

Система не является полной, т.к. функция f(x) не непрерывна.

8. f(x)= -signx

1. На  функция кусочно-непрерывная и негладкая

Стационарные точки: х*=0.

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=1,-5,5:

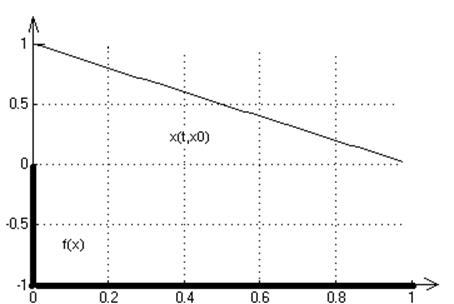
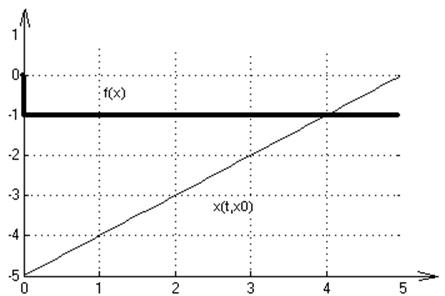
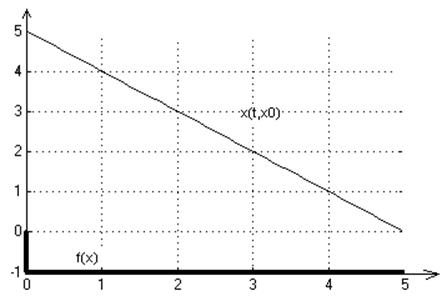
3. На множестве Х решение существует и единственно.

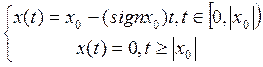
Система является полной, т.к. решения системы определены для любых начальных условий.

4. Положение равновесия х*=0 не является устойчивым, т.к. система не является полной ни в одной из его окрестностей.

9. f(x)= signx

1. На  функция кусочно-прерывная и негладкая

Стационарные точки: х*=0.

Сингулярных точек нет.

2. Графики переходных процессов для начальных условий: х0=1,-5,5:

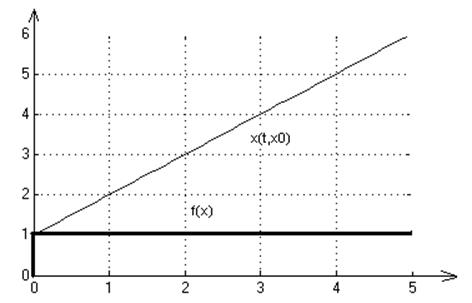
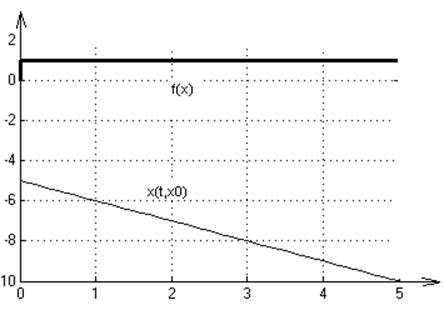
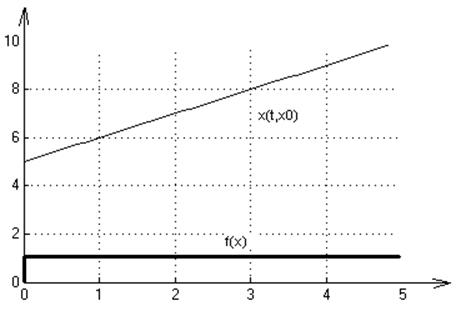
3. На множестве Х решение существует и единственно.

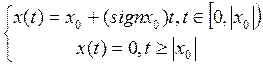
Система является полной, т.к. решения системы определены для любых начальных условий.

4. Положение равновесия х*=0 не является устойчивым, т.к. система не является полной ни в одной из его окрестностей.