Исследование нелинейных систем второго порядка, содержащих объект управления и линейный регулятор

Лабораторная работа № 2

Фазовые портреты нелинейных систем и особенности нелинейной динамики

Цель работы.

Ознакомление с нелинейными системами второго порядка, содержащие объект управления

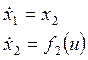
и линейный регулятор

,

где - коэффициенты обратных связей.

Исходные данные:

Исходная система 2-го порядка 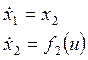 представлена на рисунке 1.1.

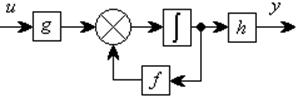
Рисунок 1.1 – Вид системы 2-го порядка

Порядок выполнения работы

1. Исследовать линейную систему, для которой . По заданным значениям корней:

(а) ,

(б) ,

(в)

характеристического полинома  рассчитать коэффициенты обратных связей . Найти положения равновесия. Построить фазовые портреты системы в области .

Линейная система

ОУ:

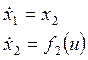
Регулятор:

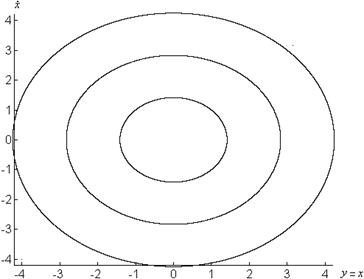
Фазовые портреты системы представлены на рисунках 1.2, 1.3.

 

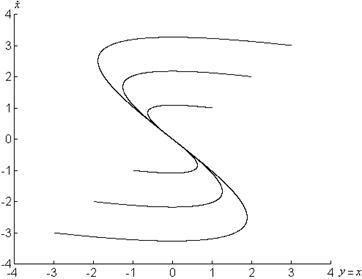
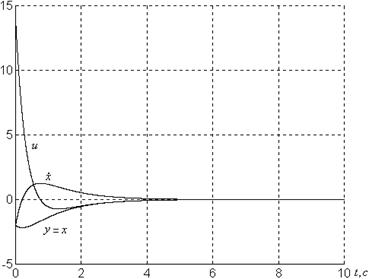
а)

 

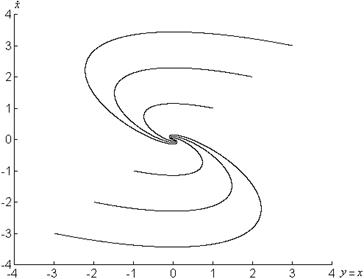
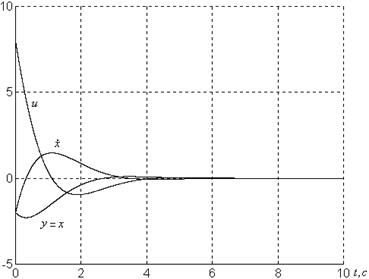
б)

Рисунок 1.2 – Графики системы  при

а) , б)

  

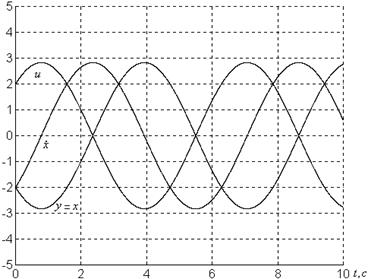
в)

Рисунок 1.3 – График системы  при

в)

2. Исследовать две гладкие нелинейные системы, для которых  и , а коэффициенты обратной связи  выбраны, как указано в п.1 (варианты а, б, в).

1) Нелинейная система

ОУ:

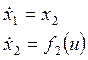
Регулятор:

Особенности нелинейной динамики:

а)

тип переходного процесса – апериодический, затухающий;

система является асимптотически устойчивой;

инвариантные множества - , ;

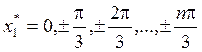аттракторы – точечные – четные стационарные точки , ;

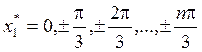области притяжения:

при , 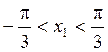- область притяжения для ,

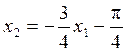при , , следовательно  и 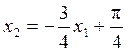- сепаратриссы.

б)

тип переходного процесса – колебательный, затухающий;

система является асимптотически устойчивой;

инвариантные множества - ,;

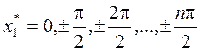аттракторы – точечные – четные стационарные точки , ;

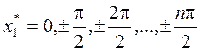области притяжения:

при , 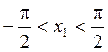- область притяжения для ,

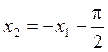при , , следовательно  и 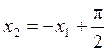- сепаратриссы.

в)

тип переходного процесса – колебательный, незатухающий;

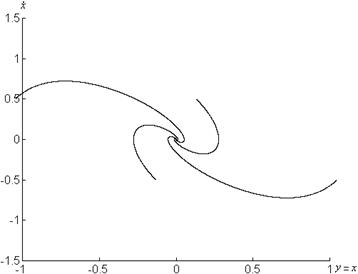
Фазовые портреты системы представлены на рисунке 1.4.

 

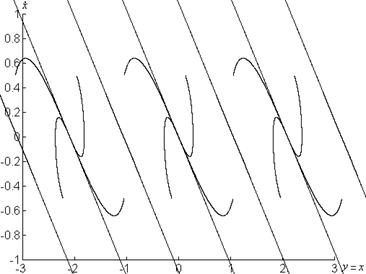
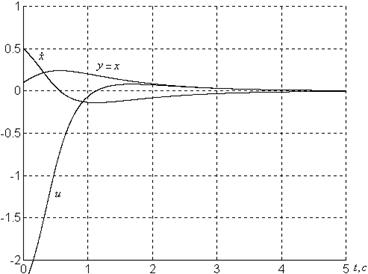
a)

 

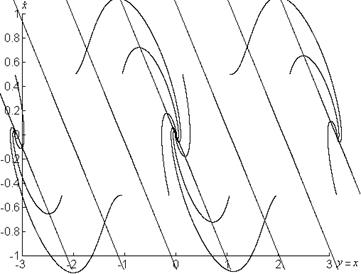
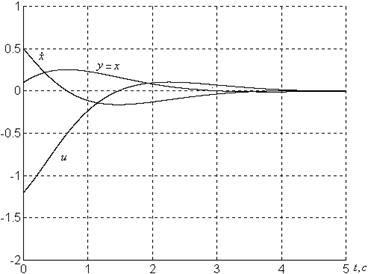
б)

 

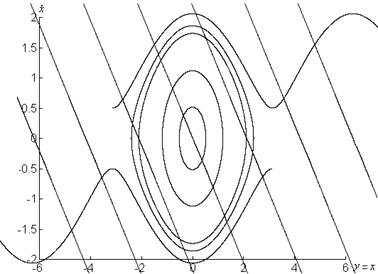
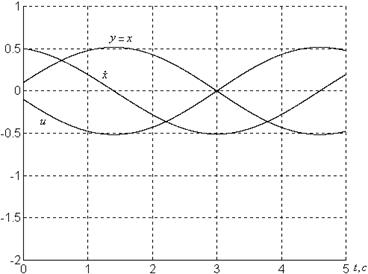
в)

Рисунок 1.4 – Графики системы  при

а) , б) , в)

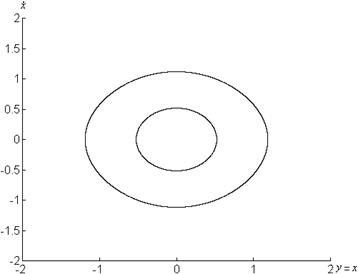
Векторные поля системы представлены на рисунке 1.5.

  

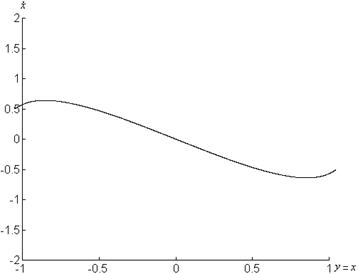
а)                                                           б)

в)

Рисунок 1.5 – Графики системы  при

а) , б) , в)

2) Нелинейная система

ОУ:

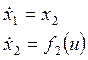
Регулятор:

Особенности нелинейной динамики:

а)

тип переходного процесса – апериодический, затухающий;

система является асимптотически устойчивой;

инвариантные множества - , ;

аттракторы - стационарная точка ,  и кривая -собственное подмногообразие;

области притяжения:

всё пространство ;

б)

тип переходного процесса – колебательный, затухающий;

система является асимптотически устойчивой;

инвариантные множества - , ;

аттракторы - стационарная точка ,  и кривая -собственное подмногообразие;

области притяжения:

всё пространство ;

в)

тип переходного процесса – колебательный, незатухающий;

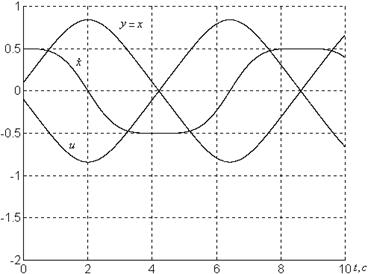
Фазовые портреты системы представлены на рисунках 1.6, 1.7.

 

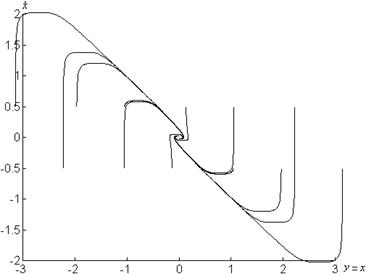
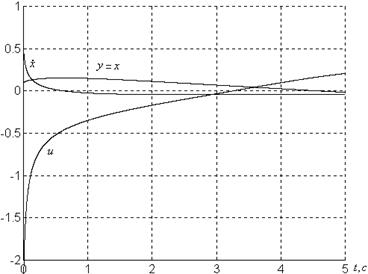
а)

Рисунок 1.6 – Графики системы  при

а)

 

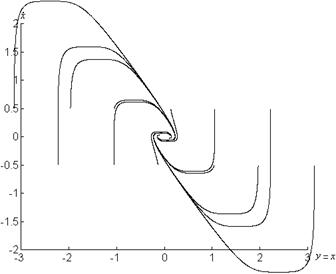
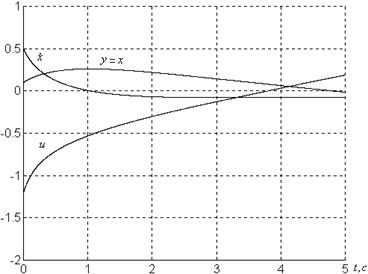
б)

 

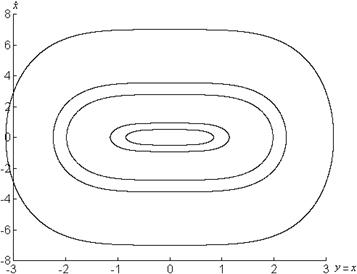
в)

Рисунок 1.7 – Графики системы  при

б) , в)

Векторные поля системы представлены на рисунке 1.8, 1.9.

 

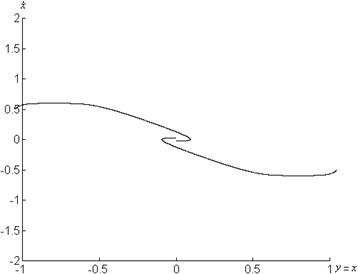
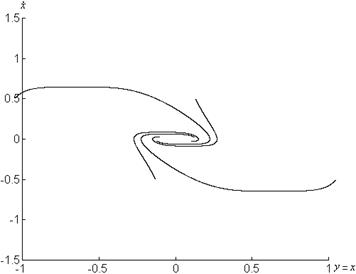
а)                                                          б)

Рисунок 1.8 – Графики системы  при

а) , б)

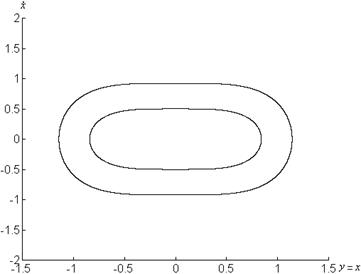
в)

Рисунок 1.9 – График системы  при

в)

Вывод:

   В результате выполнения работы были исследованы нелинейные системы второго порядка.

Появление нелинейностей в регуляторе может привести к изменению групповых свойств системы, так например, к появлению множества как устойчивых, так и нет положений равновесия, т.е. множества областей с различными свойствами, что может привести к нежелательным режимам работы, а также влиять на динамические свойства системы, искажать траектории движения, показатель качества и т.п. Подробный анализ нелинейных систем может выявить наилучшую стратегию управления.