


















Арзамасский Политехнический Институт
Филиал Нижегородского Государственного Технического Университета
кафедра "Прикладная математика"
Курсовая работа
Модель антиблокировочной системы тормозов, объединенной с системой активной подвески
Выполнил студент гр. АСПМ 3–1 Воробьёв С. П.
Арзамас, 2006 г.
АРЗАМАССКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
|
к курсовой работе
Воробьёв Сергей Павлович
Факультет Информатики Электроники Приборостроения
Кафедра Прикладная математика
Группа АСПМ 3-1
Дата защиты «_______» ________________________2006 г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
АРЗАМАССКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
Кафедра Прикладная математика
Заведующий кафедрой
(подпись) __________ Пакшин П. В.
(дата) ____________
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
Руководитель
(подпись) __________ Фомин Д. М.
(дата) ____________
Студент
(подпись) __________ Воробьёв С. П.
(дата) ____________ (гр.) АСПМ 3-1
Проект защищён (дата) _____________
Протокол № ____________________
С оценкой ______________________
2006 г.
Содержание
Введение. Постановка задачи………………………………………..……….…3
Раздел 1. Модель системы и её динамика ………………...…………………...4
Раздел 2. Нелинейная обратношаговая схема…………………………….…....7
Раздел 3. Результаты моделирования…………………………………..……...12
Заключение. Выводы…………………………………………………………....16
Библиографический
список……………………………………….……..…..…17
Введение. Постановка задачи
В работе исследуется модель антиблокировочной системы тормозов, совмещенной с активной подвеской. Хотя тормозной путь может быть уменьшен за счет тормозного момента передаваемого от дисковых или барабанных тормозов, время торможения и тормозной путь могут быть ещё более сокращены, если совместно с АБС применяется активная подвеска, доставляющая колёсам дополнительную нормальную силу. Для каждой подсистемы должен быть спроектирован свой контроллер, а также разработан интегрирующий алгоритм, координирующий действия этих двух подсистем. В результате объединения АБС с системой активной подвески действительно улучшаются характеристики тормозной системы, а именно уменьшаются время торможения и тормозной путь.
Во время торможения, если вертикальная нормальная сила возрастает (что эквивалентно возрастанию массы автомобиля), сила трения между колесами и дорожным покрытием тоже возрастает, что способствует сокращению тормозного пути. Тем не менее, нормальная сила, естественно, не может изменяться, поэтому активная подвеска должна послужить тем механизмом, который будет это обеспечивать. Выбирая подходящим образом объединяющий алгоритм, можно связать нормальную силу с тормозным моментом.
Структура данной работы следующая. В разделе 1 вводится модель АБС с активной подвеской и анализируется её динамика. Затем разрабатываются нелинейные обратношаговые контроллеры этих двух подсистем, а алгоритм, координирующий их действия, вводится в разделе 2. В разделе 3 результаты моделирования рассматриваемой системы сравниваются с результатами, показываемыми транспортными средствами, оборудованными только АБС, и автомобилями, в которых для торможения к колесам прикладывается постоянный момент.
Раздел 1. Модель системы и её динамика
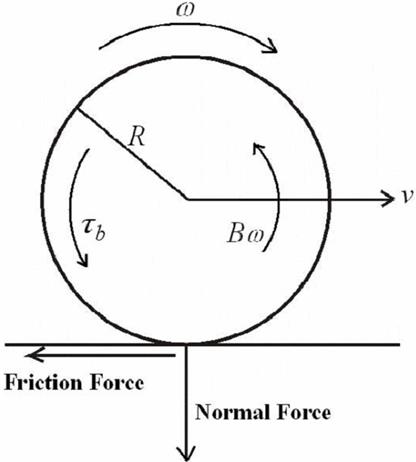
Рис. 1: Модель тормозной системы для одного колеса
Модель тормозной системы для одного колеса автомобиля показана на рис. 1. В соответствии со вторым законом Ньютона, динамика процесса торможения автомобиля может быть представлена следующими уравнениями:
![]()
![]() ,
,
![]() ,
,
![]() , где
, где
![]() — общая масса, состоящая из масс
автомобиля и колес,
— общая масса, состоящая из масс
автомобиля и колес, ![]() — скорость автомобиля,
— скорость автомобиля, ![]() — угловая скорость,
— угловая скорость, ![]() — тормозной момент, приложенный к дисковым
или барабанным тормозам,
— тормозной момент, приложенный к дисковым
или барабанным тормозам, ![]() — момент инерции
колеса,
— момент инерции
колеса, ![]() — коэффициент трения в подшипниках колеса,
— коэффициент трения в подшипниках колеса,
![]() — коэффициент трения между шинами и
дорогой,
— коэффициент трения между шинами и
дорогой, ![]() — вертикальная нормальная сила,
— вертикальная нормальная сила, ![]() — радиус колеса,
— радиус колеса, ![]() —
аэродинамический коэффициент автомобиля. В дополнении к этому тормозной момент
регулируется давлением от педали тормоза
—
аэродинамический коэффициент автомобиля. В дополнении к этому тормозной момент
регулируется давлением от педали тормоза ![]() , причем
, причем
![]() является постоянной времени, а
является постоянной времени, а ![]() — коэффициентом усиления торможения.
— коэффициентом усиления торможения.
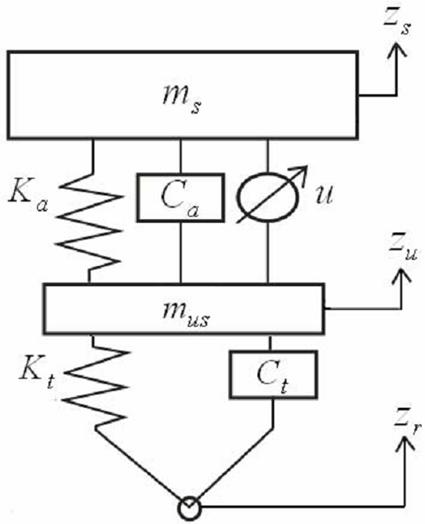
Рис. 2: Модель активной подвески для одного колеса
Кроме того, рис. 2 иллюстрирует модель активной подвески для одного колеса. Уравнения движения для этой модели могут быть записаны следующим образом:
![]()
![]() ,
,
![]() , где
, где
![]() и
и ![]() —
перемещения кузова автомобиля и колеса,
—
перемещения кузова автомобиля и колеса, ![]() и
и ![]() — коэффициенты жесткости пружин,
— коэффициенты жесткости пружин, ![]() и
и ![]() —
коэффициенты демпфирования,
—
коэффициенты демпфирования, ![]() — неровности дороги, и
— неровности дороги, и ![]() — управляющая сила от гидроусилителя. Из
(1) и (2) имеем
— управляющая сила от гидроусилителя. Из
(1) и (2) имеем
![]() ,
,
![]() ,
,
![]() где
где ![]() есть ускорение
свободного падения. Отметим, что коэффициент трения
есть ускорение
свободного падения. Отметим, что коэффициент трения ![]() в (1)
является функцией проскальзывания колеса
в (1)
является функцией проскальзывания колеса ![]() и
определяется как
и
определяется как
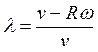 .
.
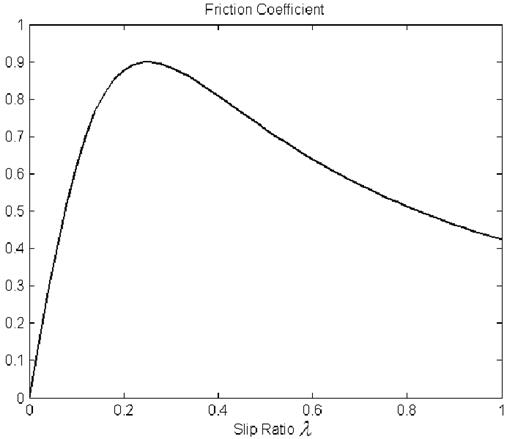
Рис.3: Связь между коэффициентом трения и проскальзыванием колеса
Связь между коэффициентом трения ![]() и проскальзыванием колеса
и проскальзыванием колеса ![]() , показанная на рис.3, может быть
аппроксимирована следующей функцией:
, показанная на рис.3, может быть
аппроксимирована следующей функцией:
![]()
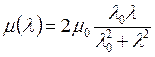 , где
, где
![]() — оптимальное значение проскальзывания,
доставляющее максимум функции
— оптимальное значение проскальзывания,
доставляющее максимум функции ![]() :
: ![]() . Отметим, что различным дорожным условиям
соответствуют свои значения
. Отметим, что различным дорожным условиям
соответствуют свои значения ![]() .
.
Вводя переменные состояний ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() , объединенную систему (1), (2) можно
представить в виде
, объединенную систему (1), (2) можно
представить в виде
![]()
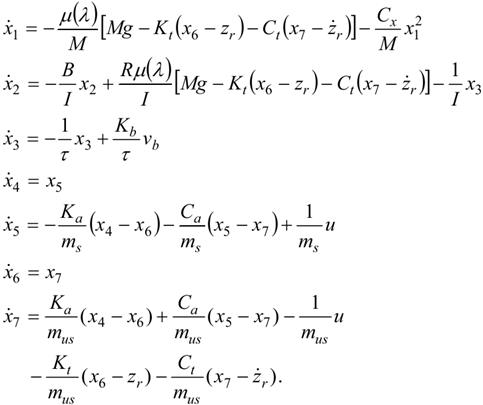
Раздел 2. Нелинейная обратношаговая схема
В соответствии с динамикой системы,
исследованной в разделе 1, цель управления объединенной АБС заключается в
поддержании коэффициента проскальзывания ![]() близким
к его оптимальному значению
близким
к его оптимальному значению ![]() , что ведет к быстрейшему
уменьшению скорости автомобиля до нуля, т. е. его полной остановке. Это
достигается за счет разработки контроллеров (одного для АБС, другого для
активной подвески), основанных на нелинейных обратношаговых схемах. В начале
введем регулируемые переменные для описания процесса торможения
, что ведет к быстрейшему
уменьшению скорости автомобиля до нуля, т. е. его полной остановке. Это
достигается за счет разработки контроллеров (одного для АБС, другого для
активной подвески), основанных на нелинейных обратношаговых схемах. В начале
введем регулируемые переменные для описания процесса торможения
![]()
![]() ,
,
Производная от переменной ![]() вычисляется
как
вычисляется
как
![]()
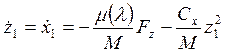 .
.
Из (3) находим желаемую угловую скорость
![]()
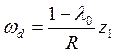 ,
,
![]() которой соответствует
коэффициент проскальзывания, доставляющий максимум коэффициенту трения. С
выбором управления
которой соответствует
коэффициент проскальзывания, доставляющий максимум коэффициенту трения. С
выбором управления ![]() фазовая переменная ошибки
определяется как
фазовая переменная ошибки
определяется как
![]() .
.
Следовательно, производная от переменной ![]() находится следующим образом:
находится следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.