Одномерная модель потока, потеря напора

Одномерная модель потока, потеря напора

В общем случае, течение жидкости осуществляется в пространстве по трем координатам. Соответственно, по этим координатам существуют проекции вектора абсолютной скорости и ускорения.

В большинстве практических случаев течение жидкости можно рассматривать как одномерное течение жидкости в одной пространственной координате, при этом перемещения, скорости и ускорения по остальным двум координатам пренебрежимо малы.

При движении жидкости по трубам основные изменения координаты, скорости и ускорения происходят вдоль оси трубопровода, изменения кинематических параметров вдоль остальных координат можно считать пренебрежимо малыми.

В XIX веке эмпирическим путем была получена формула для определения потери напора на трение при движении жидкости в трубопроводе в следующем виде

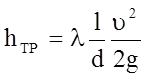.                                            (5.69)

Эта формула получила название формулы Дарси-Вейсбаха.

В записанной формуле:

l - коэффициент гидравлического трения;

l - длина трубопровода;

d - диаметр трубопровода;

u - скорость потока жидкости.

При наличии местных сопротивлений, принимая во внимание, что местные потери практически не зависят ни от длины трубы, ни от ее диаметра, нетрудно получить формулу

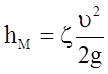,                                                   (5.70)

где z - безразмерный коэффициент, так называемый коэффициент местных потерь; u - скорость потока после прохода через местное сопротивление.

Данная формула получила название формулы Вейсбаха.

Определим общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов.

Для прямолинейного равномерного движения жидкости в горизонтальном трубопроводе постоянного сечения из уравнения Бернулли имеем

.

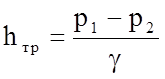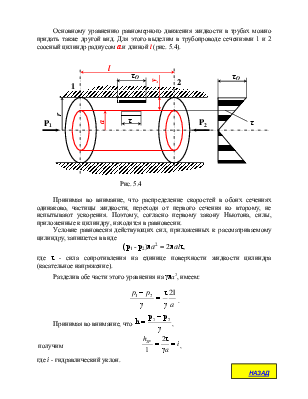
Основному уравнению равномерного движения жидкости в трубах можно придать также другой вид. Для этого выделим в трубопроводе сечениями 1 и 2 соосный цилиндр радиусом а и длиной l (рис. 5.4).

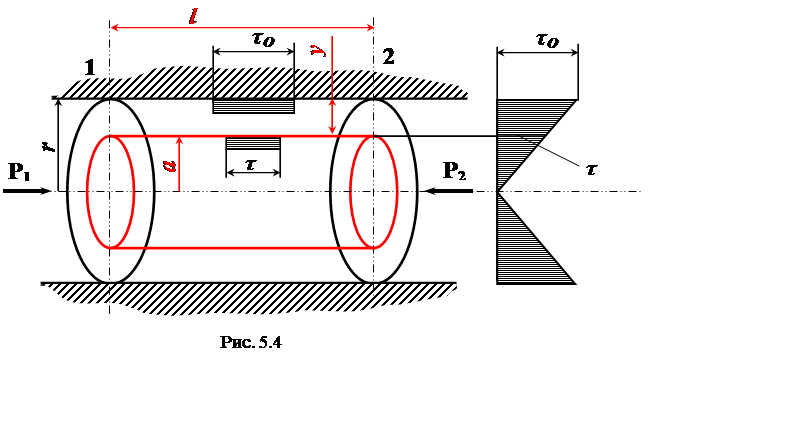Принимая во внимание, что распределение скоростей в обоих сечениях одинаково, частицы жидкости, переходя от первого сечения ко второму, не испытывают ускорения. Поэтому, согласно первому закону Ньютона, силы, приложенные к цилиндру, находятся в равновесии.

Условие равновесия действующих сил, приложенных к рассматриваемому цилиндру, запишется в виде

(р₁ - р₂)pа² = 2pаlt, где t - сила сопротивления на единице поверхности жидкости цилиндра (касательное напряжение).

Разделив обе части этого уравнения на gpа², имеем:

.

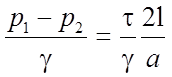Принимая во внимание, что 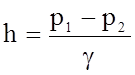, получим  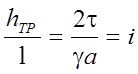                                             , где i - гидравлический уклон.

Данное уравнение может быть записано в виде:

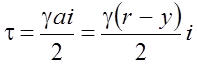,                                    (5.71)

где y - расстояние от стенки трубы до рассматриваемого слоя.

Касательное напряжение в соответствии с полученной формулой распределяется по линейному закону: на оси трубы оно равно нулю и максимальное значение на стенке при y = 0

 .

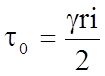Отсюда следует, что

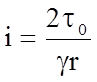       .                                              (5.72)

Уравнение для определения i представляет собой общее выражение для потерь напора при равномерном движении жидкости в трубопроводах круглого сечения. Это уравнение в одинаковой мере применимо как к ламинарному, так и к турбулентному режимам.

Уравнение для вычисления t можно представить в виде:

.

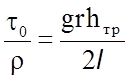Подставляя в данное выражение значение h_тр из формулы Дарси-Вейсбаха имеем

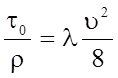.                                            (5.73)

Величина t₀/r имеет размерность квадрата скорости. Если ввести обозначение

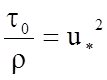, где u_* - скорость касательного напряжения на стенке, то уравнение (5.73) запишется в виде:

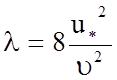
или          .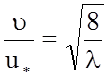

Таким образом, квадрат отношения динамической скорости к средней