Исследование истечения жидкости через отверстия и насадки

Истечение жидкости через отверстия и насадки

Исследование истечения жидкости через отверстия и насадки имеют большое практическое значение, т.к. результаты этих исследований находят применение при решении многих технических задач (при измерении расхода жидкости, при расчете и создании сильной, дальнобойной и компактной струи, при конструировании сопел, форсунок и др.).

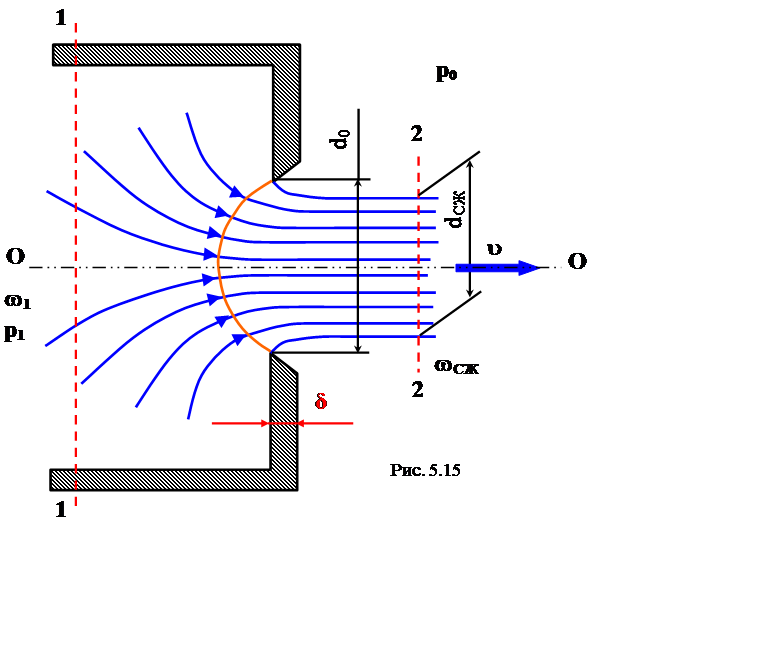Рассмотрим вначале явление истечения капельной жидкости из круглого отверстия диаметром d₀ в тонкой вертикальной стенке сосуда. Стенка считается тонкой, если ее толщина d < 0,2 d₀ (рис. 5.15).

Давление в сосуде полагаем постоянным и равным р₁. Истечение жидкости происходит из сосуда в атмосферу с давлением р₀. Площадь отверстия w₀, площадь сечения сосуда w₁.

Экспериментальные исследования позволили установить, что на расстоянии 0,5 диаметра струи она имеет наименьшую площадь сечения .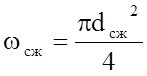

Величина коэффициента сжатия струи 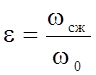 зависит от отношения 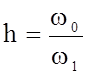 называемого степенью сжатия, здесь w₁ - площадь поперечного сечения сосуда.

В обычных условиях при истечении воды из малых отверстий в больших резервуарах коэффициент сжатия струи находится в пределах  e = 0,61‑0,63.

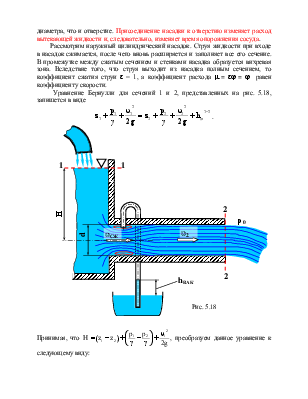
Для определения скорости истечения жидкости запишем уравнение Бернулли для сечений 1 и 2, причем сечение 2 проведем через наиболее сжатый участок струи w_сж:

.

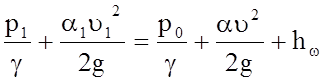Потери напора между сечениями 1 и 2 определяются по формуле Вейсбаха

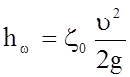, где z₀ - коэффициент сопротивления отверстия.

Принимая, что в первом приближении a₁ = a = 1 имеем:

.

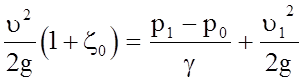Решая это уравнение относительно u, находим:

.

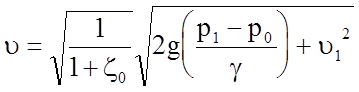Разделив обе части равенства на u, получим:

.

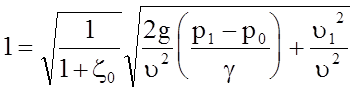Принимая во внимание, что Q = u₁w₁ = uw_сж = idem, преобразуем записанную выше формулу к виду:

.

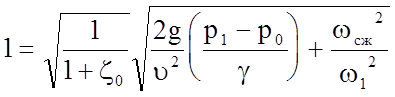Имея ввиду, что

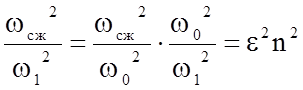
и возводя обе части записанного уравнения в квадрат, получим:

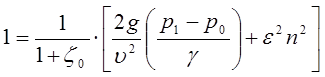, откуда .

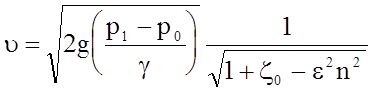Вводя обозначение ,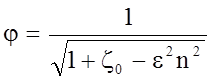

Получаем:

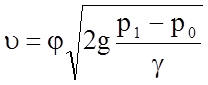,                                            (5.84)

где j - коэффициент скорости.

В случае малого отверстия (n ® 0), выражение для скорости истечения будет выглядеть следующим образом:

.

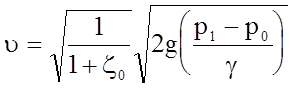При малом влиянии вязкости z₀ =0; j = 1, и тогда получим:

.

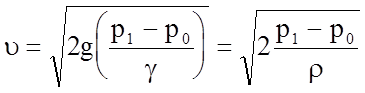При истечении воды и воздуха обычно принимают j = 0,97‑0,98;  z₀ = 0,06, т.е. всего около 2‑3% располагаемой разности давлений затрагивается на преодоление сопротивлений.

Расход жидкости, выходящей из отверстия, находим по формуле

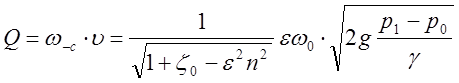.        (5.85)

          Вводя обозначение 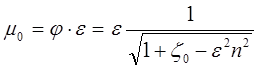, получаем:

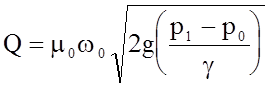, где m₀ - коэффициент расхода отверстия.

При истечении из малых отверстий (n ® 0) .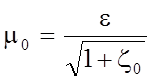

При истечении воды и воздуха коэффициент расхода m₀ принимают равным 0,6.

Значительный интерес представляет случай истечения жидкости при переменном уровне. Подобные задачи встречаются при вытекании жидкости из баков, бассейнов, резервуаров.

Рассмотрим простейший случай истечения жидкости в атмосферу через отверстие площадью w в дне сосуда призматической формы площадью W (рис. 5.16).

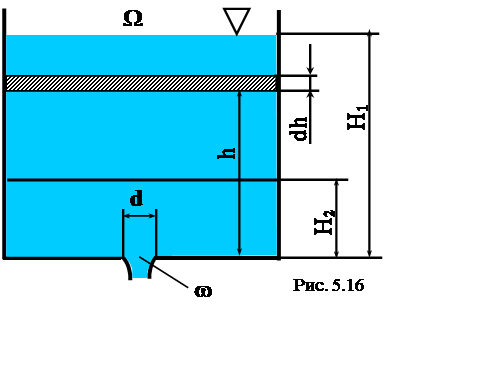Движение жидкости является неустановившимся, т.к. напор изменяется с течением времени и, следовательно, меняется расход вытекающей жидкости. За бесконечно малый промежуток времени dt, в течение которого уровень в сосуде опустится на величину dh, течение можно считать установившимся.

За это время из отверстия вытекает объем жидкости dW = Qdt, или:

.

С другой стороны, вытекающий объем можно представить также в виде:

dW = - Wdh.

Знак “-” берется потому, что dW представляет положительную величину, а dh - отрицательную. Приравнивая оба выражения для dW, получим:

 или .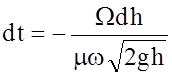

Интегрируя от Н₁ до Н₂ определяем время опорожнения сосуда: