Основные дифференциальные уравнения движения невязкой жидкости

Основные дифференциальные уравнения движения невязкой жидкости

Выделим в потоке жидкости элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (рис. 4.2).

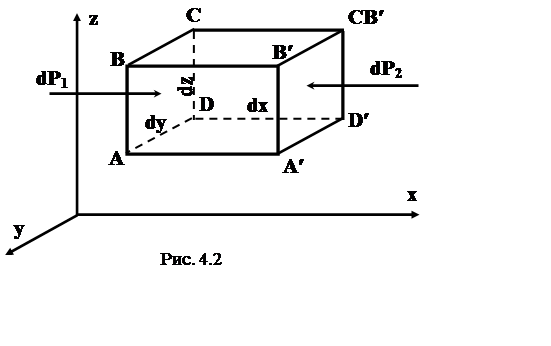Запишем второй закон Ньютона для массы жидкости в этом объеме сначала в проекциях на ось ох

mj_x = R_x,                                                  (4.21)

где масса m = rdxdydz, а проекция ускорения .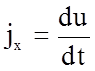

Принимая во внимание, что

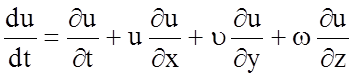,                           (4.22)

имеем

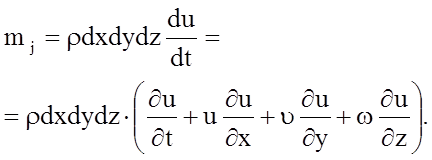                     (4.23)

Проекция силы давления на боковую грань АВСD запишется в виде

dP₁ = pdydz,                                             (4.24)

где p - среднее давление в пределах указанной грани.

          Среднее давление в пределах грани А¢В¢С¢D¢

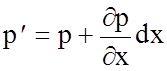                                               (4.25)

и, следовательно, сила давления на эту грань

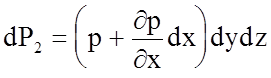.                                          (4.26)

Сумма проекций поверхностных сил на боковые грани

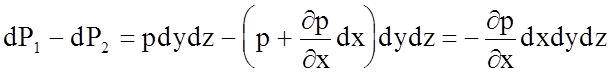.                  (4.27)

Проекцию объемных сил F_x на ось ох можно записать в виде

F_x = rdxdydzX.                                            (4.28)

Тогда, с учетом вышеизложенного, имеем:

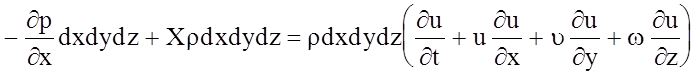.     (4.29)

Относя к единице массы (сокращая на r×dxdydz) получим:

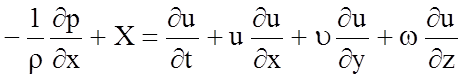.                          (4.30)

Аналогичные результаты получаются и для других осей.

В результате получаем следующую систему уравнений.

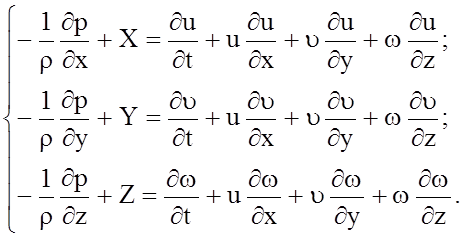                      (4.31)

Данная система уравнений носит название системы уравнений Эйлера для движения сплошной изотропной среды (капельной и газообразной жидкости).

В систему из 3-х уравнений входят пять неизвестных функций:

·  u, n, w, p и r.

Вследствие этого, для возможности решения системы, ее необходимо дополнить еще двумя уравнениями: сплошности и состояния.