Интегрирование уравнений движения. Уравнение Бернулли для потока жидкости с поперечным сечением конечных размеров

Интегрирование уравнений движения

Интегрирование уравнений Эйлера возможно для двух случаев: потенциального движения и установившегося движения в поле потенциальных сил.

Интегрирование уравнений Эйлера для потенциального потока.

Напомним, что для потенциального движения компоненты вихря w_x=w_y=w_z=0. Учитывая это, необходимо уравнения Эйлера преобразовать таким образом, чтобы они содержали компоненты вихря, что и приведет к их значительному упрощению по вышеназванной причине.

Выражение для полной скорости V через ее проекции запишется в виде:

V = u² + u² + w²,                                          (4.32)

А частные производные по x, y, z - в виде:

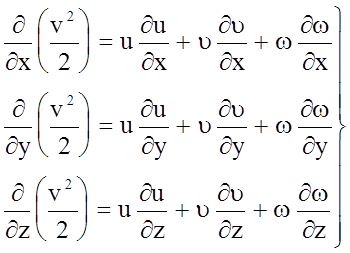.                           (4.33)

Вычитая соответственно из левой и правой частей уравнения движения соответственно левые и правые части записанных выражений, получаем

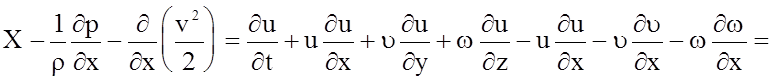
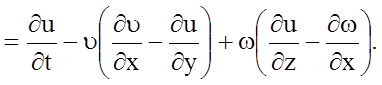                                                          (4.34)

Принимая во внимание, что

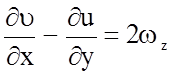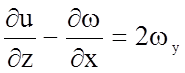;  ,                            (4.35)

имеем:

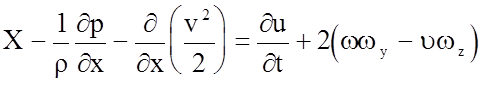   .                       (4.36)

 

Аналогично в проекциях на оси oy и oz :

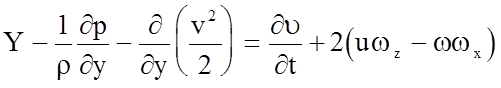;                     (4.37)

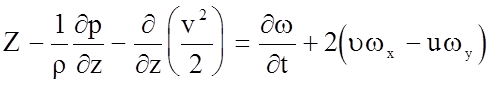.                      (4.38)

Для потенциальных движений система уравнений Эйлера преобразуется к виду

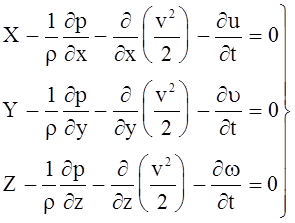.                              (4.39)

Пусть объемные силы имеют потенциал, и проекции ускорения объемных сил записываются в виде:

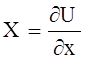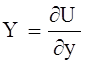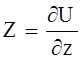; ; ,                                 (4.40)

где U - силовая функция.

Необходимо отметить, что существует функция Р(x, y, z), удовлетворяющая следующим условиям

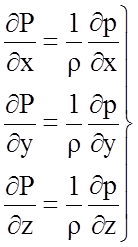,                                        (4.41)

т.е. условно:

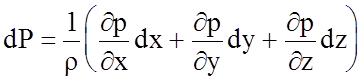                              (4.42)

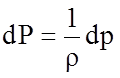или   .                                          (4.43)

Эта функция имеет вид:

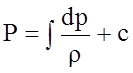.                                       (4.44)

Интеграл может быть найден при r = const или r = f(p). Для потенциального движения имеем

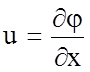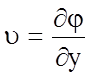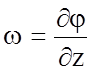; ; .                                     (4.45)

Поэтому

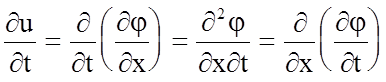;                           (4.46)

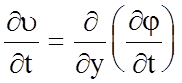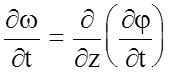; .                              (4.47)

С учетом вышеизложенного, имеем:

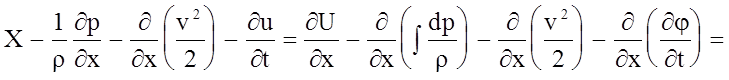
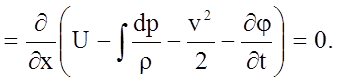                                                                (4.48)

Полная система уравнений запишется в виде:

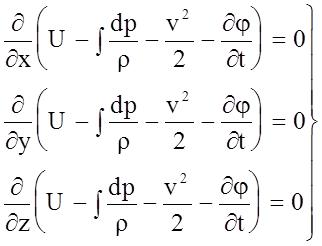.                            (4.49)

Вводя обозначение

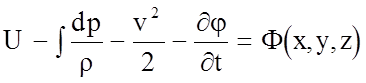                              (4.50)

получаем:

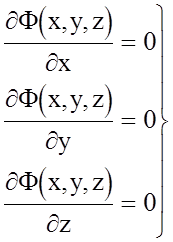               .                                            (4.51)

Умножая эти уравнения соответственно на независимые величины dx, dy, dz и затем складывая получим:

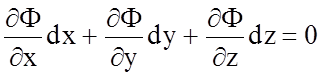.                                   (4.52)

Отсюда следует F = С(t)

     или 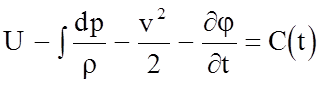                 .                                    (4.53)

Данная величина носит название интеграла Лагранжа. Интеграл Лагранжа постоянен для некоторого конкретного момента времени во всей области движения жидкости, но может меняться с течением времени.

Если у объемных сил действуют только силы тяжести, координатная ось вертикальная и направлена вверх, то Х = 0, Y = 0 и Z = - g, откуда

dU = Xdx + Ydy + Zdz = - gdz;                                     (4.54)

U= - gz.                                                         (4.55)

Для установившегося движения несжимаемой жидкости имеем

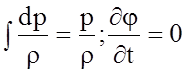     .                                               (4.56)

Интеграл Лагранжа в данном случае имеет вид:

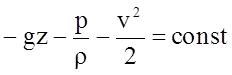                                             (4.57)

  или 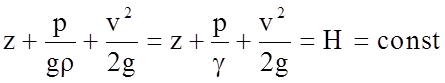          .                            (4.58)

Данное уравнение по форме идентично полученному ранее уравнению Бернулли. Однако между ними имеется существенное различие. Уравнение Бернулли показывает, что сумма трех слагаемых левой части не меняется только вдоль данной элементарной струйки, но может меняться для различных струек; при этом движение жидкости может быть как вихревым, так и потенциальным.

Уравнение, полученное из интеграла Лагранжа, справедливо только для потенциального потока, для которого постоянная Н не зависит от координат, а поэтому остается неизменной в пределах всего потока.

Интегрирование в случае установившегося движения

При установившемся движении частные производные скорости по времени равны нулю

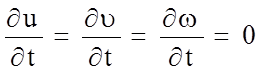                                        (4.59)

и уравнение движения записывается в виде:

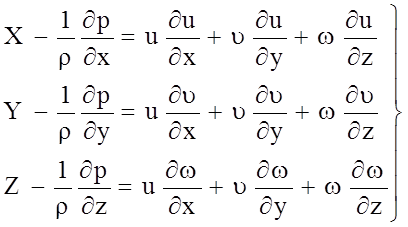.                          (4.60)

Для установившегося движения линии тока совпадают с траекториями движения частиц жидкостей и, следовательно, с элементарными струйками. Проекция dx перемещения жидкости вдоль элементарной струйки может быть определена как  dx = udt.

Умножив слагаемые I-го уравнения системы (4.60) на dx, имеем

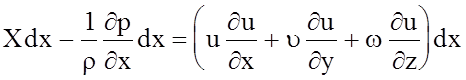.                       (4.61)

 

Преобразуем правую часть данного уравнения

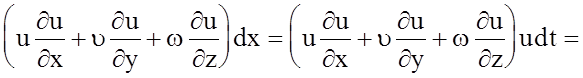
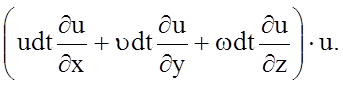=                                                   (4.62)

Учитывая, что ndt = dy  и  wdt = dz, исследуемое выражение запишется в виде:

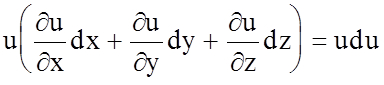,                           (4.63)

где du - полный дифференциал компонента и скорости частицы, определяемый вдоль элементарной струйки.

Имея в виду, что 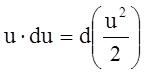, получаем:

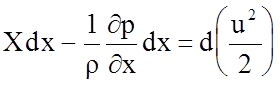.                                         (4.64)

По аналогии следующие уравнения системы (4.60) запишутся в виде:

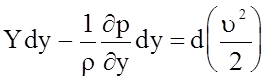      ;                                   (4.65)

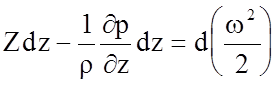      .                                   (4.66)

Складывая левые и правые части записанных уравнений, получаем

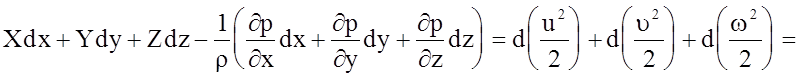
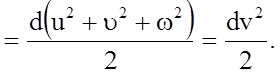                                                                                  (4.67)

Принимая, что             Xdx + Ydy + Zdz = dU;                                        (4.68)

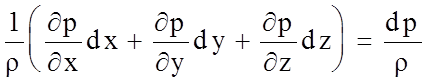 ,                                       (4.69)

имеем:

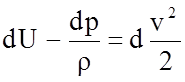.                                            (4.70)

Если движение происходит под действием сил тяжести