Динамическая игра преследования с «линией жизни» с участием космических аппаратов с двигателями малой тяги - солнечными парусами

Санкт-Петербургский государственный университет

Факультет прикладной математики - процессов управления

Салахиева

Марина

Рафиковна

Группа    452__

Практическая работа по дисциплине

«Моделирование социально-экономических систем.»

Тема: Динамическая игра преследования  с «линией жизни»

 с участием космических аппаратов с двигателями  малой тяги - солнечными парусами.

Преподаватель Малафеев О. А.

Санкт-Петербург

2010

Введение.

Рассматриваются управляемые космические аппараты (КА) с солнечными парусами (СП) на кеплеровских орбитах. Управление полетом КА осуществляется путем изменения угла установки СП относительно солнечных лучей. Будем считать, что в начальный момент времени КА уже выведены на свои орбиты и им задана начальная скорость.

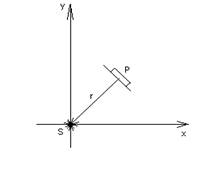
[5] Рассмотрим случай, когда парус плоский и ориентируется в пространстве так, чтобы он был всё время перпендикулярен лучам, идущим от Солнца (рисунок). Будем полагать, что ракетный двигатель космического корабля выключен. Будем считать, что в начальный момент времени КА уже выведены на свои орбиты и им задана начальная скорость. Найдём траекторию, по которой будет в этом случае двигаться корабль.

Введём следующие обозначения:  - площадь паруса,  - расстояние паруса от центра Солнца,  - среднее расстояние от Земли до Солнца. Сила, с которой солнечные лучи отталкивают парус, может быть вычислена по формул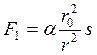е: ,            где - коэффициент пропорциональности, который может быть найден экспериментально. Этот коэффициент называют константой светового давления. Число  показывает с какой силой давят солнечные лучи на перпендикулярную с ним площадку, имеющую площадь 1 м² и расположенную вблизи Земли. Можно принять, что для абсолютно чёрного паруса . Произведение  - это суммарная сила, с которой солнечный свет давит на парус, когда последний находится вблизи Земли.

Обозначим через  массу космического корабля (вместе с парусом), через  - массу Солнца. Рассмотрим случай, когда влиянием других небесных тел, кроме Солнца, на корабль можно пренебречь (корабль находится далеко от них).

Выберем систему отсчёта с началом в центре Солнца и с осями, постоянно ориентированными в пространстве. Дифференциальное уравнение движения корабля относительно Солнца, очевидно, таково:

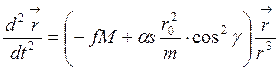    (здесь  - радиус-вектор корабля ). Введем .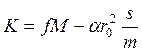     

Корабль с солнечным парусом, постоянно ориентированным перпендикулярно к солнечным лучам, будет двигаться по коническому сечению (по эллипсу, параболе или гиперболе). При этом следует считать величину  положительной, то есть площадь паруса  не очень большой.

Корабль с СП имеет следующие модели движения зависящие от площади паруса, на которую действует световое давление (т.е. от угла его ориентации по отношению к солнечным лучам) :

1)  При ,,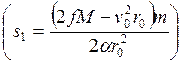 ( v₀-начальная скорость КА)  корабль движется вокруг Солнца по некоторому эллипсу. Этот эллипс будет тем более вытянутым, чем больше площадь паруса. Но с течением времени этот эллипс не будет деформироваться, не будет растягиваться (несмотря на постоянное, непрерывное давление солнечных лучей на парус!), и корабль через определённые (одинаковые) промежутки времени будет приходить к той точке своей первоначальной круговой орбиты, где был развёрнут парус.

2)  Если  или , то корабль неограниченно удаляется от Солнца (соответственно по параболе или гиперболе).

3)  Пусть  выбрано настолько большим, чтобы , то есть 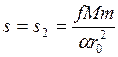. Тогда солнечное давление на парус компенсирует силу тяготения корабля к Солнцу, и корабль движется равномерно и прямолинейно.

4)  Если же площадь паруса будет больше, чем , то сила, с которой солнечное излучение отталкивает парус будет больше силы, с которой солнечная масса притягивает корабль. Корабль неограниченно удаляется от Солнца по некоторой траектории, обращённой своей выпуклостью к Солнцу.

Таким образом мы видим, что управляя углом установки паруса и меняя тем самым его активную площадь, мы можем рассматривать задачу преследования , в которой игроками являются КА с СП.

I.   Рассматривается антагонистическая игра Г(f_p⁰ , f_E⁰), в которой принимают участие два игрока  - преследователь Р и убегающий Е. f_p⁰ = (x₀ , S_p⁰),  f_E⁰ = (y₀ , S_E⁰) , здесь х₀ , у₀ суть начальные кеплеровские орбиты КА. S_p⁰, S_E⁰ –площади парусов в начальный момент времени. Продолжительность игры Т < ∞. Причем   , h(r) = 0 – заданная плоская замкнутая кривая, «линия жизни». В нашей задаче линией жизни может являться орбита какой-либо внешней планеты.

Цель игрока Р – обеспечить минимальное сближение с убегающим Е, до того как тот достигнет «линии жизни», цель убегающего Е – достичь «линию жизни» избежав до этого встречи с игроком Р.

При этом посторенние межорбитальных перелетов КА основывается на методе импульсных аппроксимаций активных участков (это возможно, если при выборе угла установки мы проверяем условие, что , s₁, s₂ вычисляются по формулам, описанным в введении).

Будем считать, что выбирая угол установки паруса, корабль получает импульс V равный величине тяги , создаваемой СП [2]. 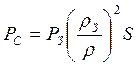, где дин/см²  –давление   солнечной   радиации   на орбите Земли; S — площадь паруса; –расстояние от Солнца до орбиты Земли. При этом не учитываются гравитационные потери маневра. Изменение скорости КА может быть записано как , где V_r –радиальная скорость КА , V_θ – тангенсальная скорость ([2]).

Рассматриваем случай ,когда игра происходит в одной плоскости.

II.  Обозначим через  множества орбит, которые могут быть достигнуты игроками Р , Е соответственно,  из начальной орбиты х₀, у₀ при активной площади S_p, S_E.