







Санкт-Петербургский Государственный Университет
Факультет Прикладной Математики – Процессов Управления
Курсовая работа по методам вычислений
Тема 6: вычисление определённого интеграла
Выполнил: Мустафин Евгений Валерьевич
Группа: 318
Проверил: Сергей Иванович Перегудин
Оценка:
ПМ-ПУ 18/12/2007
Содержание:
Постановка задачи ……………………………………………………………………………………………………………………………………3
Решение. Вариант «Ньютона-Котеса»……………………………………………………………………………………………4
Решение. Вариант «Гаусса»…………………………………………………………………………………………………………………6
Код программы на языке С++ ……………………………………………………………………………………………………………7
Результат вычислений ……………………………………………………………………………………………………………………………9
Список литературы ……………………………………………………………………………………………………………………………………9
Постановка задачи.
|
|
|
|
1 |
Вычислить
этот интеграл с точностью |
|
2 |
Вариант «Ньютона-Котеса» |
|
Построить (малую)
трёхточечную На базе построенной ИКФ (малой) построить составную и, увеличивая число разбиений на частичные отрезки mи оценивая её остаточный член по Ричардсону, добиться заданной точности. |
|
|
3 |
Вариант «Гаусса» |
|
Построить (малую)
трёхточечную интерполяционную квадратурную формулу с весовой функцией и 2.3. Оценить методическую погрешность. На базе построенной ИКФ (малой) построить составную и, увеличивая число разбиений на частичные отрезки mи оценивая её остаточный член по Ричардсону, добиться заданной точности. |
|
Решения задачи. Вариант «Ньютона-Котеса».
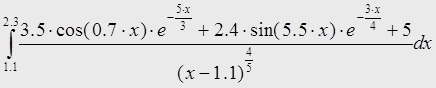 |
Нам дан интеграл вида:
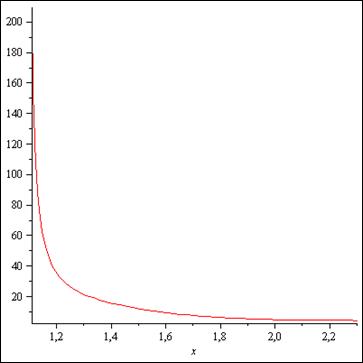 |
График подынтегральной функции выглядит так:
Видно, что при x -> 1.1 значение функции стремиться к бесконечности, это и делает невозможным вычисление интеграла обычным способом.
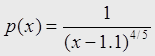 Выделим
в нём весовую функцию
Выделим
в нём весовую функцию
![]() и
гладкую функцию
и
гладкую функцию
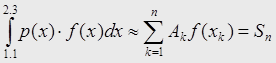 |
составим интерполяционную квадратурную формулу (ИКФ):
где
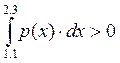
ИКФ типа Ньютона-Котеса это квадратурные формулы
с равностоящими узлами. В нашем случаи 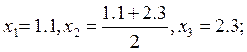
Наша задача сводится к нахождению Ак:
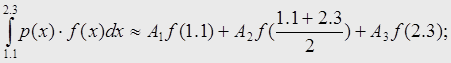 |
Алгоритм вычисления интеграла:
1. Задаём узлы (x1 x2 x3) n = 3;
2. Вычисляем моменты весовой функции
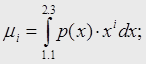
![]()
3. Решаем систему алгебраических уравнений:
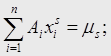
![]()
Алгебраическая степень точности будет не меньше 2.
Составная квадратурная формуластроится просто. Мы делим отрезок интегрирования на к частей и на каждом участке применяем квадратурную формулу, далее результаты складываем. Оцениваем полученные суммы интегралов методом Ричардсона.
Оценка вычисления интеграла при k-разбиений: (Для варианта Гаусса и Котеса)
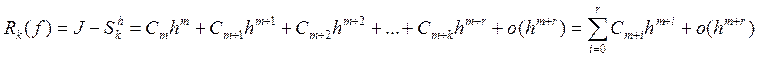
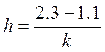 ;
;
Полагая в этой формуле h = h1, h2, … hr+2, мы получим систему алгебраических уравнений относительно переменных J, Cm, Cm+1, … ,Cm+r
Решив эту систему, мы получим оценку погрешности: метод Ричардсона.
Система будет выглядеть так:
|
k = 2 |
k = 3 |
… |
k = r |
|
|
|
|
… |
= = = … = |
|
|
|
||||
|
… |
||||
|
|
||||
Решения задачи. Вариант «Гаусса».
Также выделяем из исходного интеграла весовую функцию p(x) и функцию f(x) и составим интерполяционную квадратурную сумму:
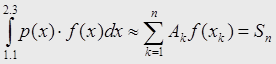 |
Здесь коэффициенты Ak и узлы xk выбираются таким образом, чтобы квадратурная формулы была точна для всех алгебраических многочленов степени 2n-1.
Алгоритм вычисления интеграла:
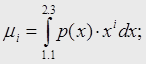
![]()
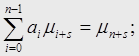
![]()
![]() которые являются узлами квадратурной формулы
которые являются узлами квадратурной формулы
4. Решаем систему уравнений для нахождения Ai
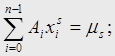
![]()
Алгебраическая степень точности будет не меньше 5.
Код программы на языке С++
#include <iostream>
#include <cmath>
#include "Matrix.h"
#include <iomanip>
#include "array.h"
using namespace std;
const double ALPHA = 4.0/5;
const double BETA = 0;
const double LEFT = 1.1;
const double RIGHT = 2.3;
const int N = 3;
const double PRECISION = 0.000001;
const double J = 27.56649553; // Интеграл, подсчитанный в Maple
double f(double x) { return 3.5 * cos(0.7 * x) * exp(-5 * x * 1/3) + 2.4 * sin(5.5 * x) * exp(-3 * x * 1/4) + 5; }
//
Вспомогательные функции - вычисленные первообразные для ![]()
double n0 (double x) { return 5*pow(x,1/5); }
double n1 (double x) { return 5/6*pow(x,6/5) + 11/2 * pow(x,1/5); }
double n2 (double x) { return 5/11*pow(x,11/5) + 2.2*5/6*pow(x,6/5) + pow(1.1, 2)*5*pow(x,1/5); }
double n3 (double x) { return 5/16*pow(x,16/5) + 1.5*pow(x,11/5) + 121/40*pow(x, 6/5) + 6.655*pow(x, 0.2); }
double n4 (double x) { return 5/21*pow(x,21/5)+1.375*pow(x,16/5)+3.3*pow(x,11/5)+1331/300*pow(x,6/5)+7.3205*pow(x,0.2);}
double n5 (double x) { return 109104.0/13549*pow(x,0.2) + 14641.0/2400*pow(x,6.0/5) + 121.0/20*pow(x,11.0/5) + 121.0/32*pow(x,16.0/5) + 55.0/42*pow(x,21.0/5) + 5.0/26 * pow(x, 26.0/5); }
// Вычисление моментов
double Nu0(double a, double b) { return n0(b - 1.1) - n0(a - 1.1); }
double Nu1(double a, double b) { return n1(b - 1.1) - n1(a - 1.1); }
double Nu2(double a, double b) { return n2(b - 1.1) - n2(a - 1.1); }
double Nu3(double a, double b) { return n3(b - 1.1) - n3(a - 1.1); }
double Nu4(double a, double b) { return n4(b - 1.1) - n4(a - 1.1); }
double Nu5(double a, double b) { return n5(b - 1.1) - n5(a - 1.1); }
void createMatrixKotes(Matrix &matrix, double *nu, double *node) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == 0) matrix.index(i, j) = 1;
if (i == 1) matrix.index(i, j) = node[j];
if (i == 2) matrix.index(i, j) = pow(node[j], 2);
}
matrix.index(i, 3) = nu[i];
}
}
// Аргументы: число разбиений и длина отрезка.
double intKotes(int m, double h)
{
double result = 0;
double a, b;
double middle;
for (int j = 0; j < m; j++)
{
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.