Проектирование рекурсивного фильтра, страница 3

Таблица №4

	1,05	1,2	1,35	1,5	1,65	1,8	1,95	2,1	2,25	2,5
	45	28,01	16,25	14,55	11,45	9,65	9,65	9,65	6,75	6,75
	-5,6	-2,6	-1,75	-1,5	-1,25	-1	-1	-1	-0,75	-0,75
n	22	12	9	8	7	6	6	6	5	5

Рис.7 График зависимости эффективной длительности от неравномерности в полосе задерживания.

Рис.8 График зависимости порядка передаточной функции от неравномерности в полосе задерживания.

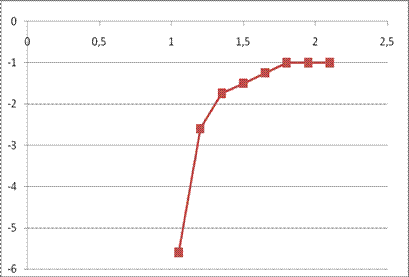
Рис.9 График зависимости фазовой задержки от относительной ширины переходной полосы АЧХ.

Исследование влияние на порядок n передаточной функции фильтра-прототипа, величину эффективной длительности  временной характеристики  и фазовой задержки шага дискретизации

Зависимости порядка передаточной функции, эффективной длительности временной характеристики, фазовой задержки от изменения относительной ширины переходной полосы АЧХ в диапазоне [0,05 с; 0,25 с] представлены в таблице №5 и на рисунках 10-12.

Таблица №5

	0,05	0,07	0,09	0,11	0,13	0,15	0,17	0,19	0,21	0,25
	14,55	14,63	15,48	15,62	15,73	15,90	15,98	16,91	17,01	17,25
	-1,5	-1,47	-1,53	-1,54	-1,56	-1,35	-1,36	-1,33	-1,47	-1,25
n	8	8	8	8	8	8	8	8	8	8

Рис.10 График зависимости эффективной длительности от неравномерности в полосе задерживания.

Рис.11 График зависимости фазовой задержки от неравномерности в полосе задерживания.

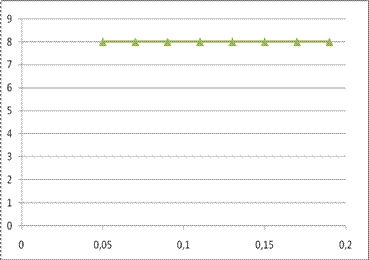
Рис.12 График зависимости порядка передаточной функции от шага дискретизации.

Исследование влияния на порядок n передаточной функции фильтра-прототипа, величину эффективной длительности  временной характеристики  и фазовой задержки коэффициента усиления(     )

 Зависимости порядка передаточной функции, эффективной длительности временной характеристики, фазовой задержки от изменения относительной ширины переходной полосы АЧХ в диапазоне [0,1; 10,0] представлены в таблице №6 и на рисунке 13.

Таблица №6

	0,1	1	2	3	4	5	6	7	8	10
	14,55	14,55	14,55	14,55	14,55	14,55	14,55	14,55	14,55	14,55
	-1,5	-1,5	-1,5	-1,5	-1,5	-1,5	-1,5	-1,5	-1,5	-1,5
n	8	8	8	8	8	8	8	8	8	8

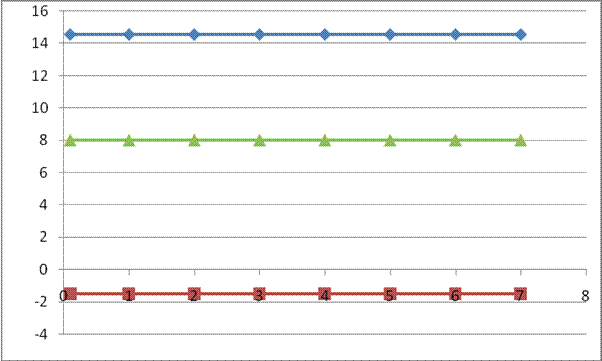
Рис.13 Графики зависимости эффективной длительности, порядка передаточной функции, фазовой задержки от коэффициента усиления.

Исследование АЧХ и ФЧХ при увеличении значения верхней частоты интервала наблюдения АЧХ и ФЧХ()

Графики АЧХ и ФЧХ при =150 р/с представлены на рисунках 14 и 15.

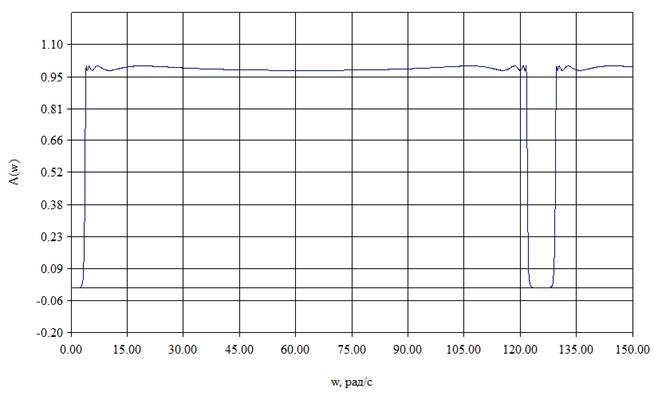
Рис.14 График амплитудной  частотной характеристики фильтра при измененных параметрах.

 

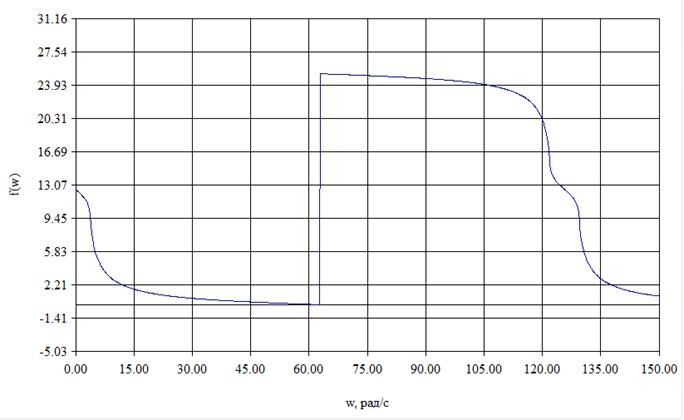
Рис.15 График фазовой частотной характеристики фильтра при измененных параметрах.

Исследование АЧХ и ФЧХ при увеличении шага дискретизации по времени()

Графики АЧХ и ФЧХ при =1 с представлены на рисунках 16 и 17.

Рис.16 График амплитудной  частотной характеристики фильтра при измененных параметрах.

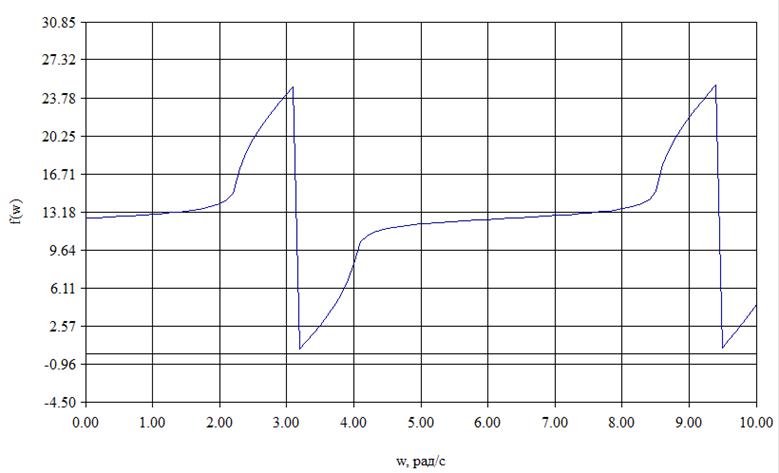
Рис.17 График фазовой частотной характеристики фильтра при измененных параметрах.

Выводы:

Спроектирован высокочастотный фильтр со следующими параметрами АЧХ: коэффициент усиления =1,0 при заданном 1,0;

нижняя граничная частота ω_ф=4 р/с при заданной 4 р/с;

ширина переходной полосы Δω_п=1,5 р/с при заданной 1,5 р/с; неравномерности в полосе пропускания Δ=0,02 при заданной 0,02

неравномерности в полосе задерживания  δ=0,00147 при заданной 0,01.

Таким образом, фильтр в целом удовлетворяет заданным параметрам. Для базового варианта параметр n = 8,  = 14,55, = -1,5.

Зависимость параметра  от  нелинейная.  С увеличением   увеличивается.  не влияет на n.

Зависимости от  монотонны. С увеличением  параметры n и  уменьшаются ,а  увеличивается.

Зависимости от параметра  имеют монотонный характер, причем с увеличением  значения n , уменьшаются, а возрастает.

Коэффициент усиления не влияет на порядок передаточной функции фильтра-прототипа, эффективную длительность переходной характеристики, фазовую задержку.