Информатика и выч. техника \ Цифровая обработка сигналов

Функционирование нерекурсивного фильтра

Страницы работы

10 страниц (Word-файл)

Скачать файл

Содержание работы

Министерство Образования и Науки Российской Федерации

Федеральное агентство по образованию

Новосибирский Государственный Технический Университет

Кафедра Автоматики

Лабораторная работа №2

Функционирование нерекурсивного фильтра

Факультет: АВТ Преподаватель: Худяков Д.С. Группа: АА-47

Студенты: Оськин С.А.

Бабенко А.А.

Вариант: 16

Дата сдачи:

Отметка о защите:

Новосибирск, 2008 г.

1. Цель работы

Посмотреть как работает нерекурсиный фильтр. Определить влияние параметров фильтра на длительность импульсной характеристики.

2. Методические указания

В режиме функционирования фильтра:

- X(K) – массив отсчетов входного сигнала фильтра , ;

- Y(K) – массив отсчетов выходного сигнала фильтра , ;

- Z(K) – массив отсчетов скорректированного выходного сигнала фильтра , , ;

- V(K) – массив отсчетов эталонного выходного сигнала фильтра , ;

- EY – ошибка фильтрации ;

- EZ – скорректированная ошибка фильтрации .

3. Исходные данные

Таблица 1

№

Тип задачи

Тип фильтра

р/с

y₀(t)

СА

ВЧФ

3,0

1,20

x₂(t)+x₃(t)

Шаг дискретизации по времени =0,05 с; шаг дискретизации по частоте =0,1 р/с; относительная неравномерность в полосе пропускания АЧХ =0,01 для нерекурсивного фильтра, относительная неравномерность в полосе задерживания АЧХ =0,01 р/с; коэффициент усиления в полосе пропускания АЧХ =1,0. Вид фильтра – нерекурсивный, =3 р/с, To=6,3 c, =0 р/с, =10 р/с.

4. Проектирование фильтра

1. Привести характеристики фильтра для базового варианта.

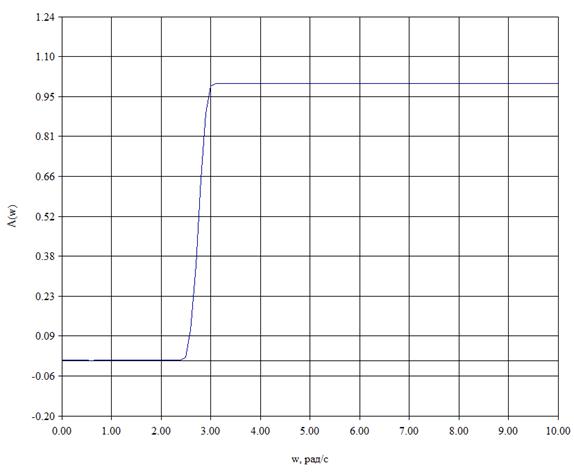
Рис.1. АЧХ фильтра с базовыми значениями.

R=3.456 L=374

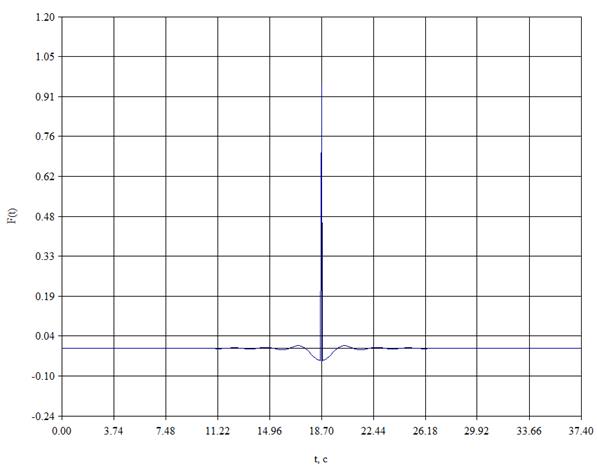
Рис.2. ИХ фильтра с базовыми значениями.

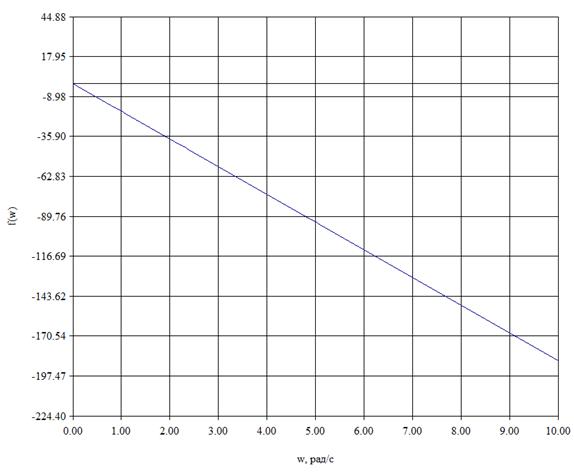
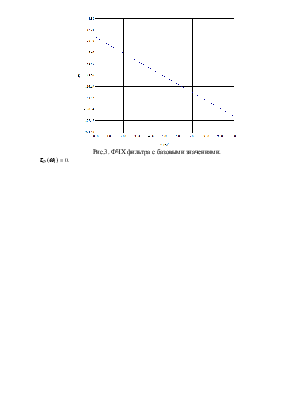
Рис.3. ФЧХ фильтра с базовыми значениями.

= 0.

5. Функционирование фильтра

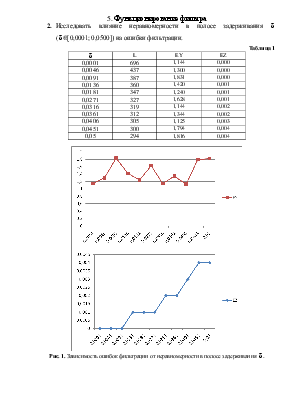
2. Исследовать влияние неравномерности в полосе задерживания ([0,0001; 0,0500]) на ошибки фильтрации.

Таблица 1

	L	EY	EZ
0,0001	696	1,144	0,000
0,0046	437	1,300	0,000
0,0091	387	1,831	0,000
0,0136	360	1,420	0,001
0,0181	347	1,240	0,001
0,0271	327	1,628	0,001
0,0316	319	1,144	0,002
0,0361	312	1,344	0,002
0,0406	305	1,125	0,003
0,0451	300	1,794	0,004
0,05	294	1,816	0,004

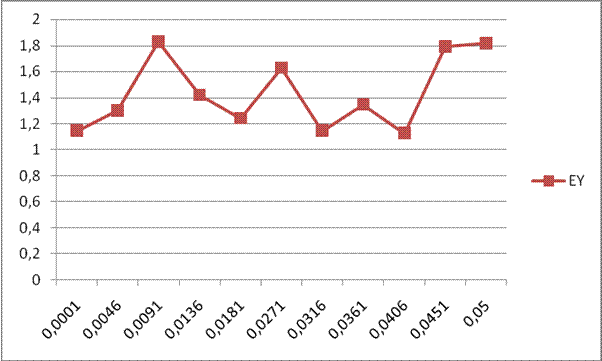
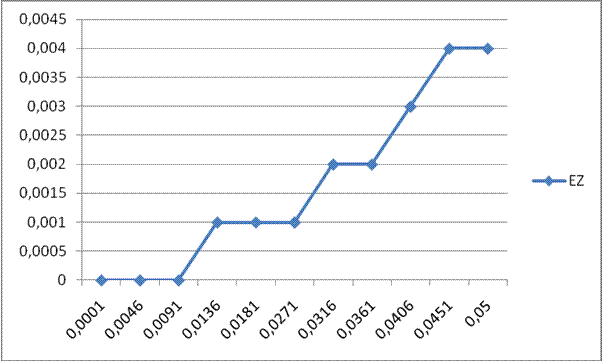
Рис. 1. Зависимость ошибок фильтрации от неравномерности в полосе задерживания .

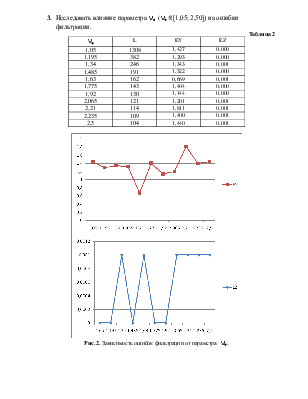
3. Исследовать влияние параметра ([1,05; 2,50]) на ошибки фильтрации.

Таблица 2

	L	EY	EZ
1,05	1308	1,427	0,000
1,195	382	1,293	0,000
1,34	246	1,343	0,001
1,485	191	1,322	0,000
1,63	162	0,669	0,001
1,775	143	1,404	0,000
1,92	130	1,144	0,000
2,065	121	1,201	0,001
2,21	114	1,811	0,001
2,235	109	1,400	0,001
2,5	104	1,440	0,001

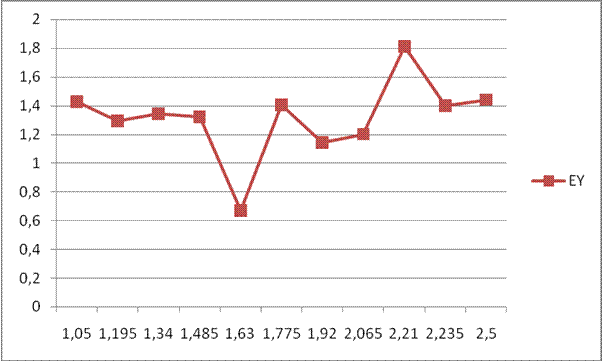
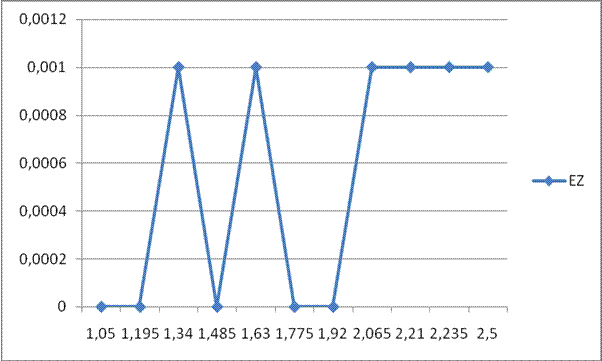
Рис. 2. Зависимость ошибок фильтрации от параметра .

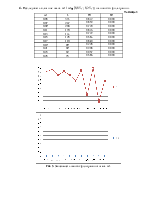
4. Исследовать влияние шага ([0,05 с; 0,25 с]) на ошибки фильтрации.

Таблица 3

	L	EY	EZ
0,05	374	0,812	0,000
0,07	267	0,859	0,000
0,09	208	0,720	0,000
0,11	170	0,816	0,000
0,13	144	0,722	0,000
0,15	125	0,583	0,000
0,17	110	0,840	0,000
0,19	99	0,228	0,000
0,21	89	0,908	0,000
0,23	82	0,057	0,000
0,25	75	0,586	0,000

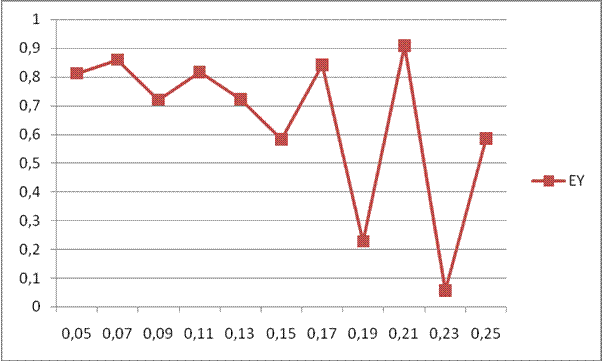
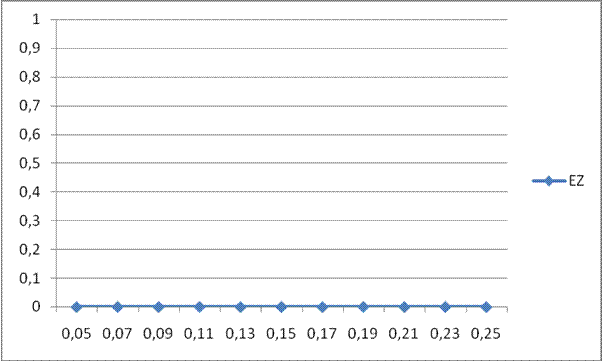
Рис. 3. Зависимость ошибок фильтрации от шага .

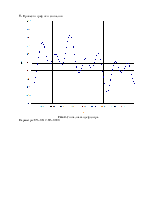
5. Привести графики сигналов.

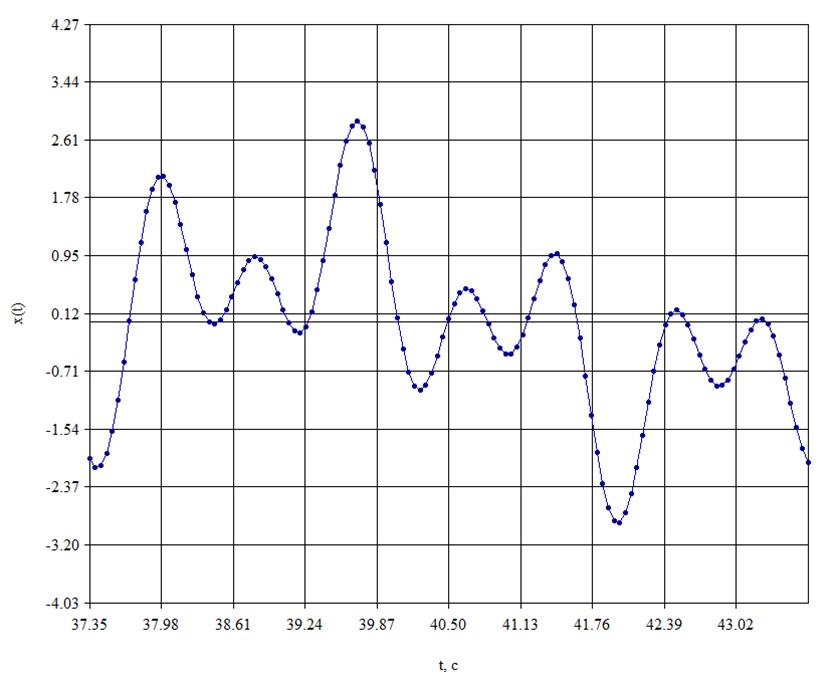
Рис. 4. Сигнал на входе фильтра.

Параметры: EY=0,812 ,EZ=0,000.

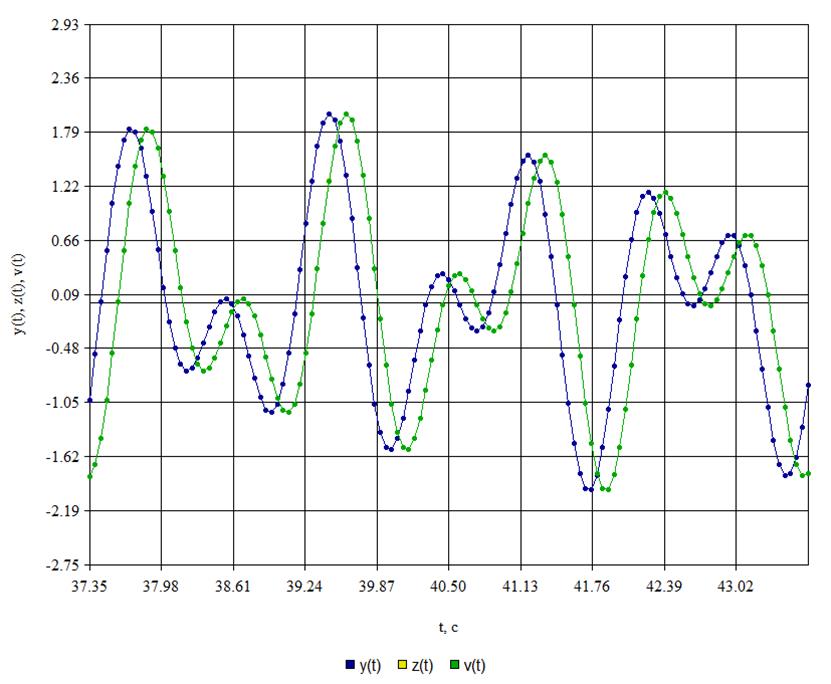
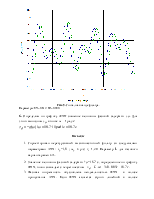
Рис. 5. Сигнал на выходе фильтра.

Параметры: EY=0,812, EZ=0,000.

6. Определим по графику ФЧХ значение величины фазовой задержки . Для этого вычислим в точке = 1рад/c:

Выводы

1. Спроектирован нерекурсивный высокочастотный фильтр со следующими параметрами АЧХ: =1,0 ; =3 р/с; =1,20. Параметр L для базового варианта равен 374.

2. Значение величины фазовой задержки =18.7 с, определенное по графику ФЧХ, точно совпадает с теоретическим – .

3. Фазовая погрешность обусловлена неидеальностью ФЧХ в полосе пропускания АЧХ. Если ФЧХ является строго линейной в полосе пропускания АЧХ (), то при введении в выходной сигнал фильтра запаздывания на величину фазовая погрешность полностью исключается. Т.о. возможность уменьшения уровня данной погрешности определяется степенью линейности ФЧХ.

4. Уровень погрешности от составляющих входного сигнала с частотными спектрами, располагающимися вне полосы пропускания, уменьшается с уменьшением неравномерности δ в полосе задерживания и ширины переходных полос АЧХ фильтра

5. В общем случае, когда составляющие входного сигнала имеют непрерывные частотные спектры, полное устранение фазовой погрешности оказывается также возможным при условии линейности ФЧХ фильтра в полосе пропускания его АЧХ. Действительно, если в полосе пропускания АЧХ справедливо соотношение , то в данной полосе частот и при введении запаздывания выходного сигнала фильтра на величину по аналогии с вышерассмотренным фазовая погрешность полностью исключается. Если же ФЧХ фильтра в полосе пропускания АЧХ является нелинейной, то за счет введения соответствующего временного запаздывания можно достигнуть лишь частичного снижения фазовой погрешности.