нежелательной неравномерности и выбросов в частотной
характеристике - имеет место так называемый эффект Гиббса. В методе
взвешивания идеальная импульсная характеристика![]() множится
на подходящую весовую функцию
множится
на подходящую весовую функцию ![]() с конечной
длительностью. Получающаяся импульсная характеристика гладко затухает до нуля.
Это приводит к значительному подавлению неравномерностей и выбросов в частотной
характеристике, характерных для прямого усечения.
с конечной
длительностью. Получающаяся импульсная характеристика гладко затухает до нуля.
Это приводит к значительному подавлению неравномерностей и выбросов в частотной
характеристике, характерных для прямого усечения.
Известно, что для метода взвешивания и некоторых других методов расчета коэффициентов КИХ-фильтров (фактически отсчетов импульсной характеристики) неравномерность в полосе пропускания и в полосе заграждения одинаковы. Поэтому рассчитывается общее требование по полосе пропускания и полосе заграждения:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
При
расчете коэффициентов КИХ-фильтра методом взвешивания сначала рассчитываются
отсчеты идеальной импульсной характеристики ![]() ,
а затем эти отсчеты умножаются на отсчеты взвешивающей функции
,
а затем эти отсчеты умножаются на отсчеты взвешивающей функции ![]() .
.
Идеальная импульсная характеристика ФВЧ описывается следующим выражением:
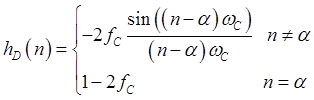 (2.3)
(2.3)
где
![]() - частота, соответствующая середине полосы
перехода.
- частота, соответствующая середине полосы
перехода.
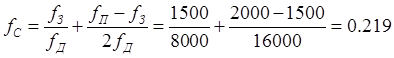 (2.4)
(2.4)
Параметр
![]() определяется как:
определяется как:
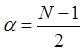 (2.5)
(2.5)
где
![]() - количество коэффициентов фильтра
(выбирается нечетным, для того чтобы импульсная характеристика
соответствовала импульсной характеристике универсального КИХ-фильтра с
линейной ФЧХ. При
такой импульсной характеристике можно реализовать произвольную АЧХ.).
- количество коэффициентов фильтра
(выбирается нечетным, для того чтобы импульсная характеристика
соответствовала импульсной характеристике универсального КИХ-фильтра с
линейной ФЧХ. При
такой импульсной характеристике можно реализовать произвольную АЧХ.).
Проведем сравнение влияния взвешивающих функций на характеристики разрабатываемого КИХ-фильтра. Также сравним характеристики фильтра, синтезируемого с использованием метода взвешивания с аналогичными характеристиками для фильтра, полученного путем прямого усечения идеализированной импульсной характеристики.
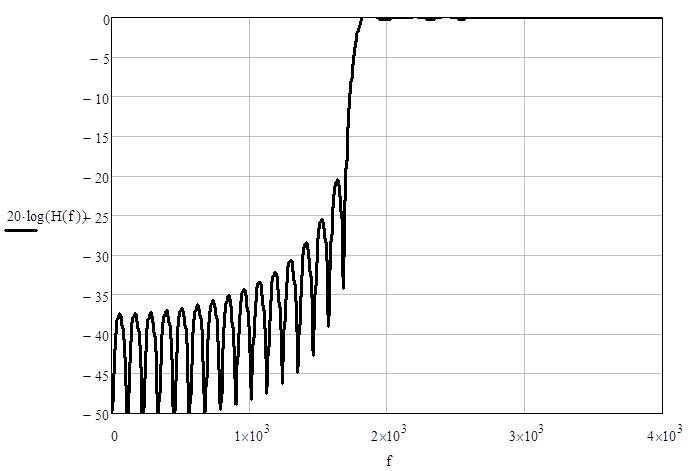
Рис. 2.1. АЧХ фильтра, полученного путем прямого усечения идеализированной импульсной характеристики до 70 коэффициентов.
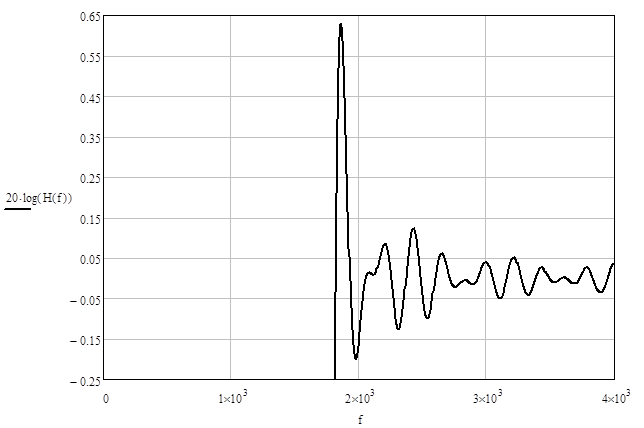
Рис. 2.2. Неравномерность в полосе пропускания.
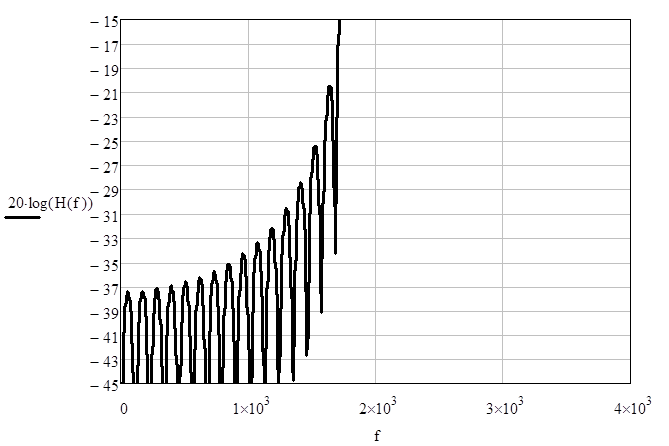
![]()
Рис. 2.3. Уровень боковых лепестков.
2.1. Взвешивающая функция Ханна
Взвешивающая функция Ханна задается следующим соотношением:
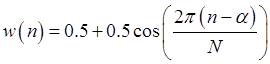 (2.1.1)
(2.1.1)
Количество коэффициентов взвешивающей функции можно определить через соотношение для нормированной ширины полосы перехода:
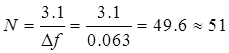 (2.1.2)
(2.1.2)
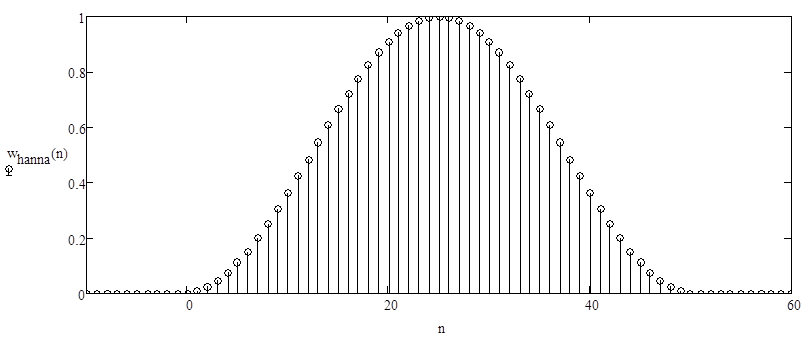 Рис. 2.1.1.
Весовая функция Ханна – временная характеристика.
Рис. 2.1.1.
Весовая функция Ханна – временная характеристика.
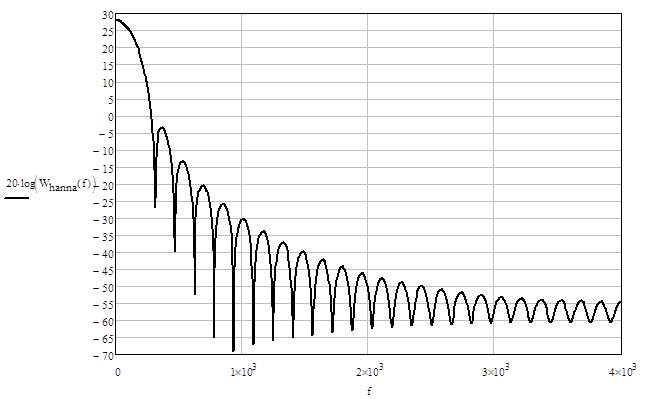
Рис. 2.1.2. Весовая функция Ханна – частотная характеристика.
Ширина основного лепестка весовой функции – 300 Гц, уровень боковых лепестков - 30 дБ по отношению к главному.
|
|
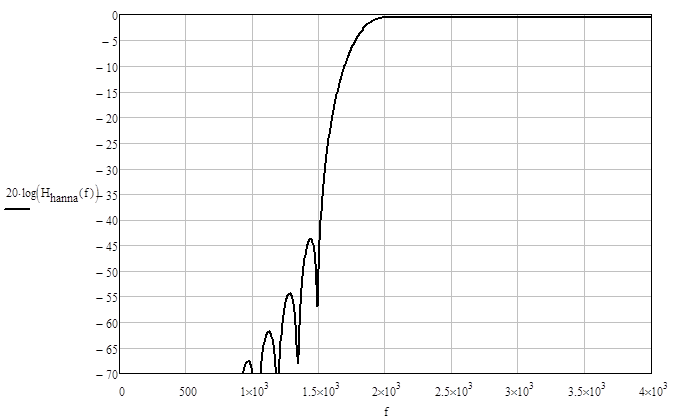
Рис. 2.1.3. АЧХ фильтра, полученного с помощью функции Ханна.
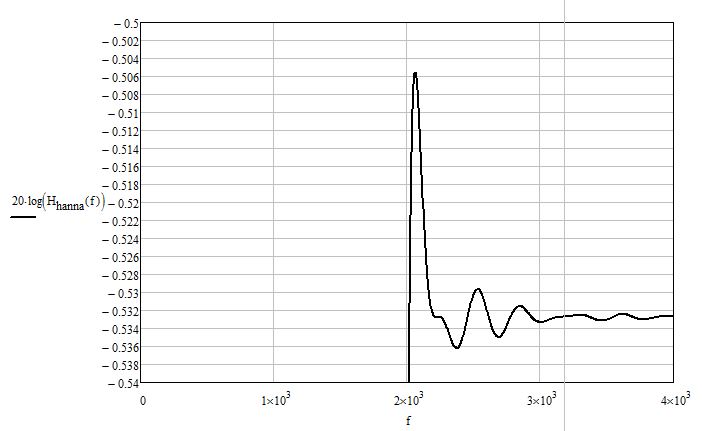
Рис. 2.1.4. Неравномерность в полосе пропускания.
Неравномерность в полосе пропускания – 0.03 дБ (рис. 2.1.4), уровень подавления боковых лепестков – -44 дБ (рис. 2.1.5), что не удовлетворяет техническому заданию, следовательно, функция Ханна не применима для реализации рассчитываемого фильтра.
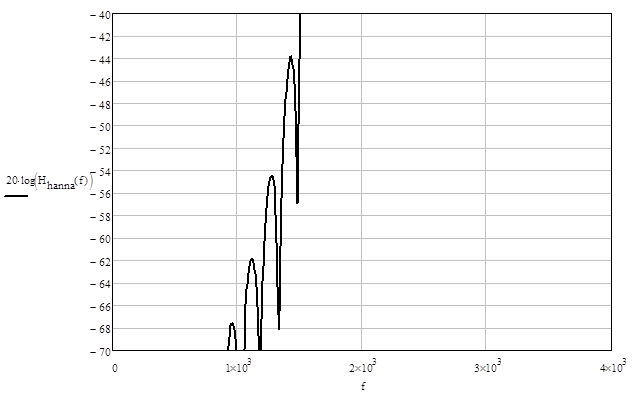
Рис. 2.1.5. Уровень боковых лепестков.
2.2. Взвешивающая функция Хэмминга
Взвешивающая функция Хэмминга задается следующим соотношением:
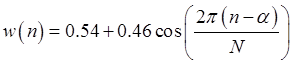 (2.2.1)
(2.2.1)
Количество коэффициентов взвешивающей функции можно определить через соотношение для нормированной ширины полосы перехода:
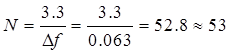 (2.2.2)
(2.2.2)
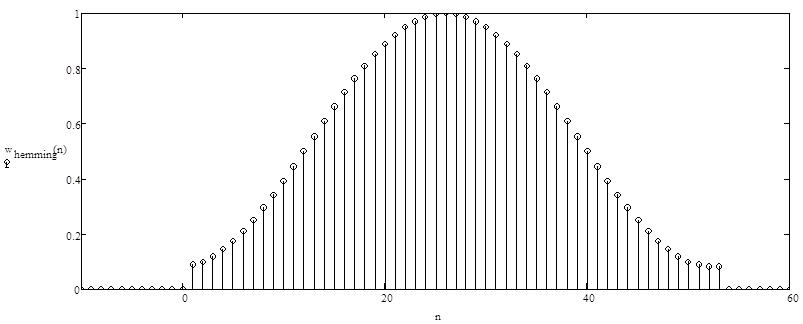
Рис. 2.2.1. Весовая функция Хэмминга – временная характеристика.
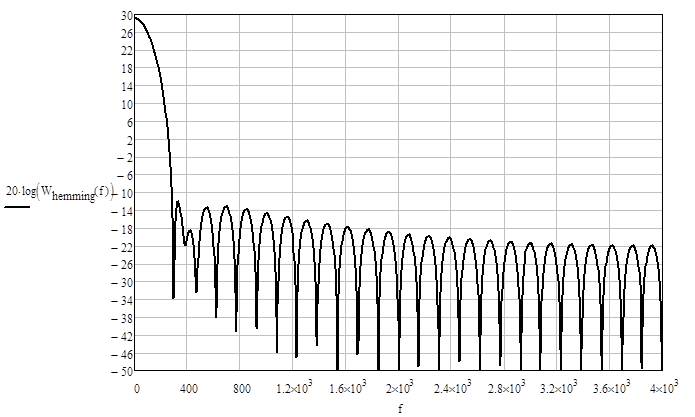
Рис. 2.2.2. Весовая функция Хемминга – частотная характеристика.
Ширина основного лепестка весовой функции – 300 Гц, уровень боковых лепестков - 42 дБ по отношению к главному.
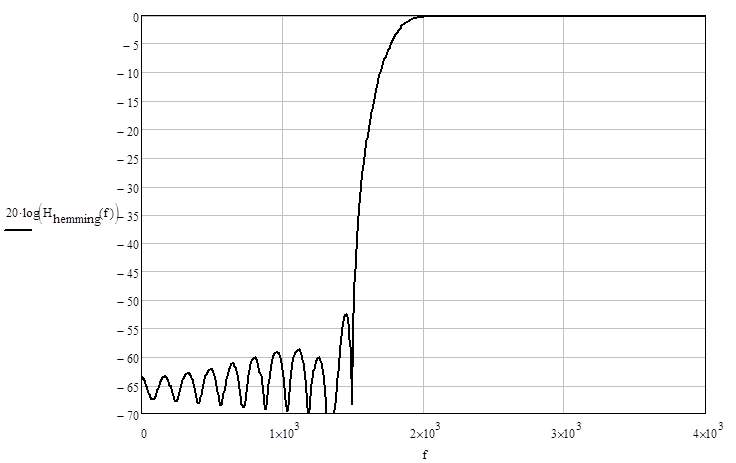
Рис. 2.2.3. АЧХ фильтра, полученного с помощью функции Хемминга.
Неравномерность в полосе пропускания – 0.022 дБ (рис. 2.2.4), уровень подавления боковых лепестков – -52.5 дБ (рис. 2.2.5), что не удовлетворяет техническому заданию, следовательно, функция Хэмминга не применима для реализации рассчитываемого фильтра.
Фильтр, рассчитанный с использованием функции Хэмминга, обладает более хорошими параметрами, по сравнению, с фильтром, рассчитанным с использованием функции Ханна.
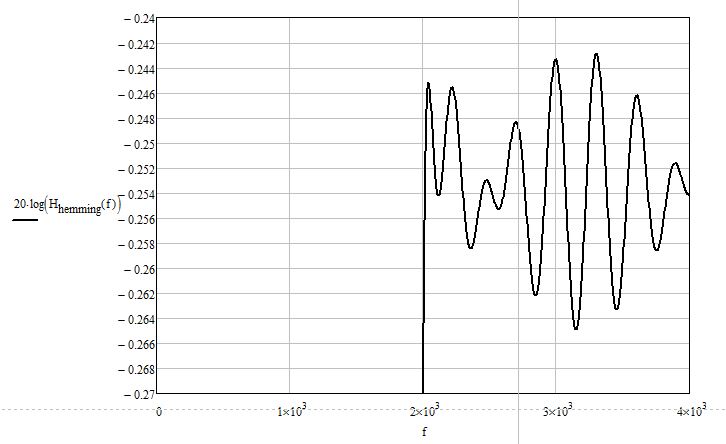
Рис. 2.2.4. Неравномерность в полосе пропускания.
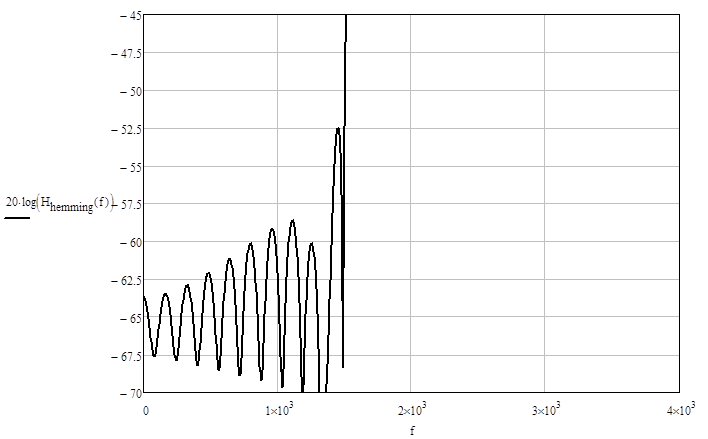
Рис. 2.2.5. Уровень боковых лепестков.
2.3. Взвешивающая функция Блэкмена
Взвешивающая функция Блэкмена задается следующим соотношением:
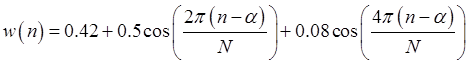 (2.3.1)
(2.3.1)
Количество коэффициентов взвешивающей функции можно определить через
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.