Задание: Составить программу вычисления определенного интеграла с автоматическим выбором шага интегрирования. Расчет интеграла различными методами, а также расчет подынтегральной и первообразной функции оформлять в виде отдельных функций. Допустимую точность вычисления вводить в функции main() с клавиатуры. Функции, рассчитывающие интеграл, кроме значения интеграла должны возвращать и количество обращений к подынтегральной функции. Полученные численным методом значения интегралов необходимо сравнить с их значением, найденным через первообразную функцию.
|
Номер варианта |
Вычисляемый Интеграл |
Первообразная функции |
Метод вычисления |
|
19 |
|
-x+tg( |
Формула Ньютона-Котеса для n=4 Формула Гаусса для n=2 |
 Алгоритмфункции nyut4()
Алгоритмфункции nyut4()
H0=0.07777778,H[4]={0.3555556,0.1333333,
0.3555556,0.1555555};
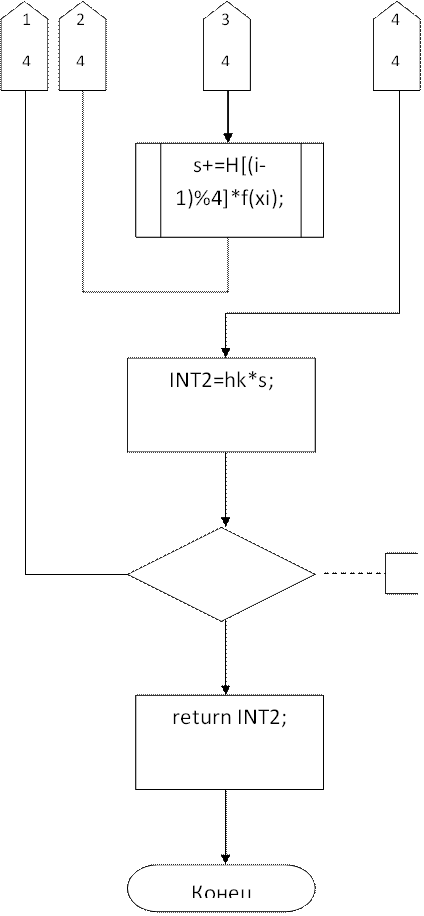
да fabs(INT1-INT2)>=eps;
нет
Алгоритм функцииgauss()
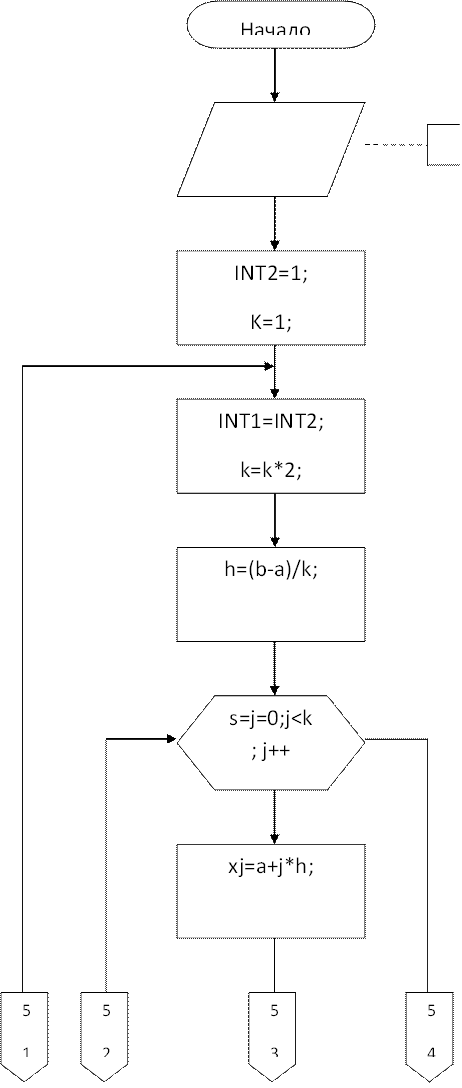
X[2]={0.2113249,0.7886751},
A=0.5;
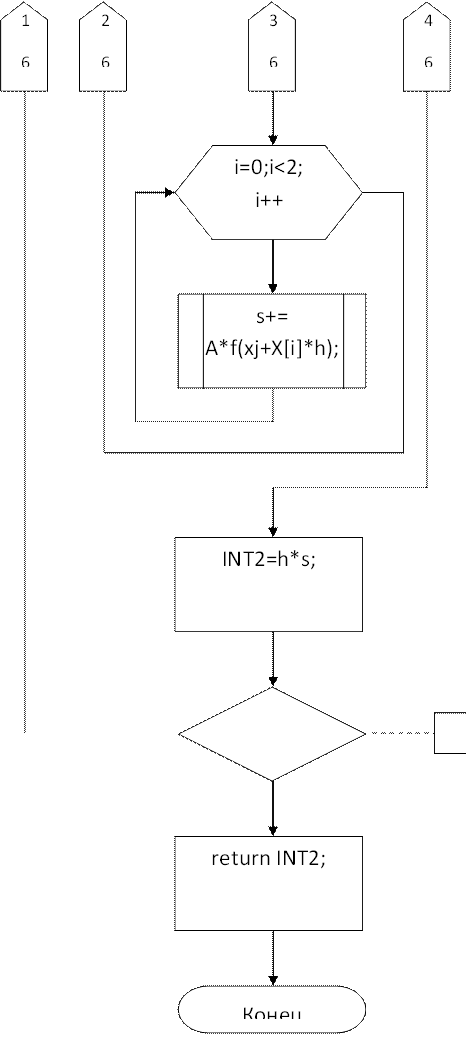
![]() да
да
fabs(INT1-INT2)>=eps;
нет
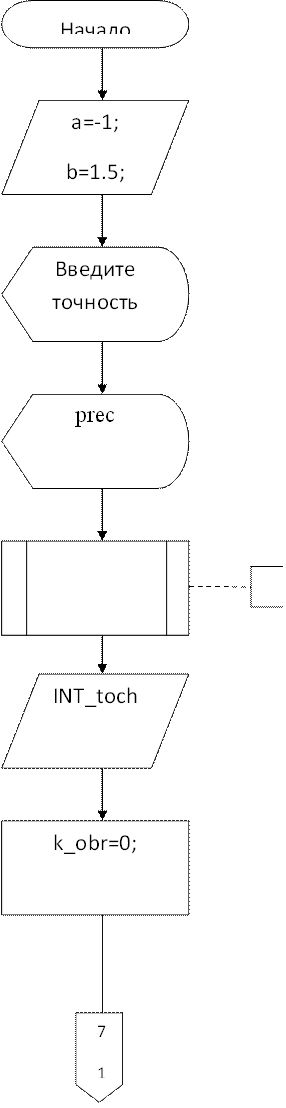 Алгоритмфункции main()
Алгоритмфункции main()
INT_toch=perv_obr(b)-perv_obr(a);
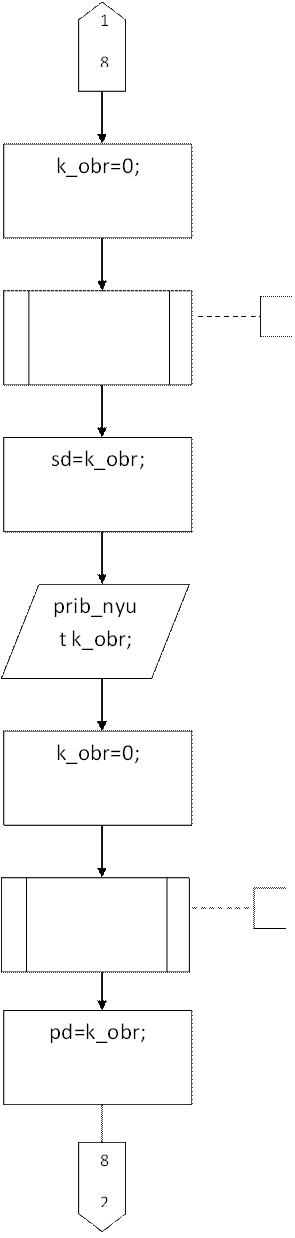 |
prib_nyut4=nyut4(a,b,fun,prec);
prib_gauss2=gauss(a,b,fun,prec);
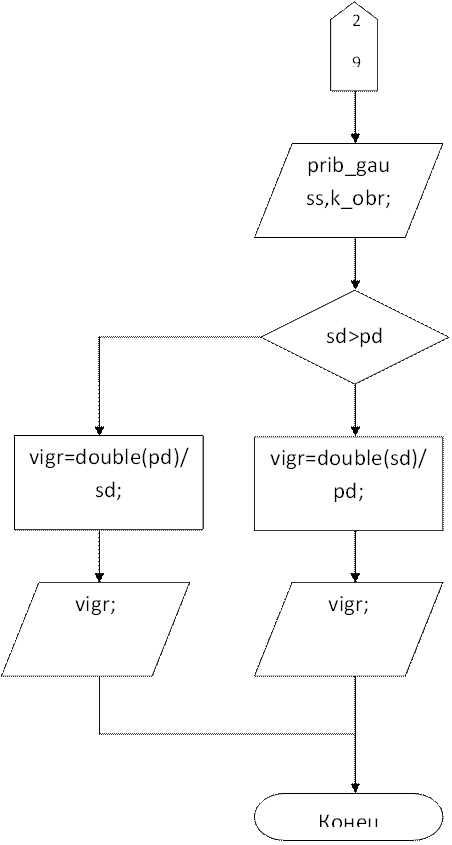
нет
да
Алгоритм функции perv_obr()
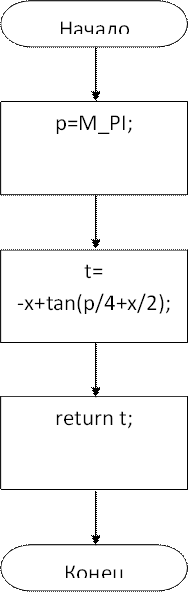 |
![]() Алгоритм функции fun()
Алгоритм функции fun()
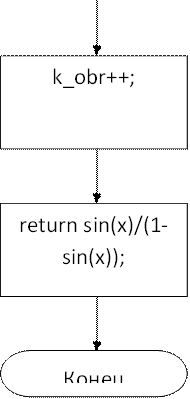 |
Текст программы.
#include<math.h>
#include<iostream.h>
#include<stdio.h>
long int k_obr;//глобальная переменная, для количества обращений
typedef double D;
D perv_obr(D x);
D fun(D x);
D nyut4(D x,D y,D f(D),D eps);
D gauss(D a,D b,D f(D), D eps);
void main()
{D a=-1,b=1.5,prib_nyut4,INT_toch,prec,prib_gauss2,vigr;
FILE *fp;
long int sd,pd;
fp=fopen("rgz1.txt","a");//открываем файл для записи результатов
cout<<"Введите точность";
cin>>prec;//вводим точность вычисления интеграла
printf("Точность =%.9lf",prec);//выводим на экран точность вычисления
fprintf(fp,"Точность=%.9lf",prec);//запись в файл точности вычисления
INT_toch=perv_obr(b)-perv_obr(a);//вычисляем точное значение интеграла
printf("\nТочное значение интеграла %.9lf",INT_toch);/*выводим на экран точное значение интеграла
fprintf(fp,"\ Точное значение интеграла %.9lf",INT_toch);//записываем в файл точное значение интеграла
k_obr=0;/*обнуляем глобальную переменную, для записи в нее количества обращений к подинтегральной функции
prib_nyut4=nyut4(a,b,fun,prec);//вызов функции вычисляющей интеграл по методу Ньютона-Котеса
sd=k_obr;//записывем количество обращений к подынтегральной функции в переменную sd
printf("\nЗначение интеграла по методу Ньютона-Котеса n=4 %.9lf Количество обращений=%ld",prib_nyut4,k_obr);/*выводим на экран значение интеграла по методу Ньютона Котеса и кол-во обращений к подынтегральной функции
fprintf(fp,"\nЗначение интеграла по методу Ньютона-Котеса n=4 %.9lf Количество обращений=%ld",prib_nyut4,k_obr);/*записываем в файл значение интеграла по методу Ньютона-Котеса и кол-во обращений к подынтегральной функции
k_obr=0;//обнуляем глобальную переменную
prib_gauss2=gauss(a,b,fun,prec);//обращение к функции считающей интеграл по методу Гаусса
pd=k_obr;//записываем количество обращений к подынтегральной функции в переменную pd
printf("\n Значение интеграла по методу Гаусса n=2 %.9lf Количество обращений=%ld",prib_gauss2,k_obr);/*выводим на экран значение интеграла по методу Гаусса и кол-во обращений к подынтегральной функции
fprintf(fp,"\n Значение интеграла по методу Гаусса n=2 %.9lf Количество обращений=%ld",prib_gauss2,k_obr); );/*записываем в файл значение интеграла по методу Гаусса и кол-во обращений к подынтегральной функции
if(sd>pd)/*Сравниваем количество обращений функции вычисляющей интеграл по методу Ньютона-Котеса с количеством обращений функции по методу Гаусса(если оно больше, то выигрывает метод Гаусса)
{vigr=double(sd)/pd;//считаем во сколько раз выигрывает метод Гаусса
printf("\Выигрыш Гаусса к Ньютону-Котесуn=%.9lf",vigr);
fprintf(fp,"\nВыигрыш Гаусса к Ньютону-Котесу=%.9lf",vigr);
}
else
{vigr=double(pd)/sd;/*считаем во сколько раз выигрывает метод Ньютона-Котеса
printf("\Выйгрыш Ньютона-Котеса к Гауссу=%.9lf",vigr);
fprintf(fp,"\n Выйгрыш Ньютона-Котеса к Гауссу =%.9lf",vigr);
}
fclose(fp);//закрываем файл, в который записывали результаты работы программы
}
D perv_obr(D x)
{D t,p;
p=M_PI;
t=-x+tan(p/4+x/2);
return t;
}
D fun(D x)
{k_obr++;//счетчик считает количество обращений к подынтегральной функции
return sin(x)/(1-sin(x));
}
D nyut4(D a,D b,D f(D),D eps)
{D INT1,INT2,s,h,hk,xi;
D H0=0.07777778,H[4]={0.3555556,0.1333333,0.3555556,0.1555555};
int k=1,i,im;
INT2=1;//присваиваем начальное значение INT2
do
{INT1=INT2;
k=k*2;//удваиваем количество разбиений
hk=(b-a)/k;
im=4*k;
h=hk/4;//шаг интегрирования для n=4
s=(f(a)+f(b))*H0;//присваиваем начальное значение интегральной сумме
for(i=1;i<im;i++)
{xi=a+i*h;//находим точки, в которых будет вычисляться подынтегральная функция
s+=H[(i-1)%4]*f(xi);//составляем интегральную сумму
}
INT2=hk*s;
}
while(fabs(INT1-INT2)>=eps);//оцениваем погрешность вычисления
return INT2;//возвращаем значение интеграла в функцию main()
}
D gauss(D a,D b,D f(D),D eps)
{D x,INT1,xj,INT2,s,h,X[2]={0.2113249,0.7886751},A=0.5;
int i,j,k=1;
INT2=1;//присваиваем начальное значение INT2
do
{INT1=INT2;
k=k*2; ;//удваиваем количество разбиений
h=(b-a)/k;//шаг интегрирования
for(s=j=0;j<k;j++)
{ xj=a+j*h;
for(i=0;i<2;i++)
{
s+=A*f(xj+X[i]*h);//считаем интегральную сумму
}
}
INT2=s*h;
}
while(fabs(INT1-INT2)>=eps); //оцениваем погрешность вычисления
return INT2;//возвращаем значение интеграла в функцию main()
}
Тестовый пример.
Точность =0.100000000
Точное значение интеграла 25.444844857
Значение Ньютона-Котеса n=4 25.445040653 Колличество обращений=510
Значение Гаусса n=2 25.443995184 Колличество обращений=508
![]() Выигрыш Гауса к Ньютону-Котесу=1.003937008
Выигрыш Гауса к Ньютону-Котесу=1.003937008
Точность =0.010000000
Точное значение интеграла 25.444844857
Значение Ньютона-Котеса n=4 25.445040653 Колличество обращений=510
Значение Гаусса n=2 25.444789028 Колличество обращений=1020
![]() Выигрыш Ньютона-Котеса к Гаусу=2.000000000
Выигрыш Ньютона-Котеса к Гаусу=2.000000000
Точность =0.000100000
Точное значение интеграла 25.444844857
Значение Ньютона-Котеса n=4 25.444845039 Колличество обращений=2048
Значение Гаусса n=2 25.444841319 Колличество обращений=2044
Выигрыш Гауса к Ньютону-Котесу=1.0019569
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.