






МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Автоматики
Индивидуальное задание №1 по курсу
«Системы автоматической оптимизации»
Факультет: АВТ
Группа: ААМ-10
Студент: Преподаватель:
Мещеряков Д. Французова Г.А.
Вариант: 9
Дата выполнения:
Отметка о защите:
Новосибирск, 2010
Задание
Рассчитать и исследовать с помощью моделирования в среде MATLAB систему экстремального регулирования (с учетом необходимых оценок производных) для объекта, математическая модель которого имеет вид:
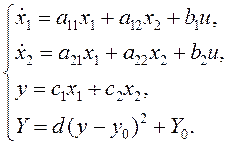
Известны
ограничения на переменные состояния и управляющее воздействие: ![]() ,
, ![]() ,
, ![]() . Заданы требования к качеству процесса
выхода на экстремум в виде следующих оценок:
. Заданы требования к качеству процесса
выхода на экстремум в виде следующих оценок: ![]() и
и ![]() .
.
Таблица 1. Исходные данные
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
-2 |
-1 |
0 |
6 |
3 |
0 |
0,5 |
1 |
2 |
50 |
100 |
600 |
2 |
30 |
Расчет системы
Математическая модель объекта в соответствии с исходными данными имеет вид:
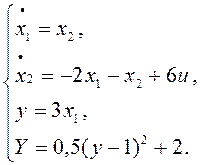
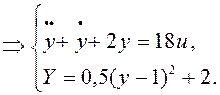
Представим данную систему в виде двухконтурной системы с предварительной стабилизацией и рассчитаем параметры внутреннего и внешнего регуляторов.
Внутренний регулятор
Во внутреннем контуре стабилизируется динамическая часть объекта, представленная в следующем виде:
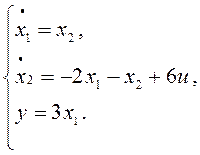
Процессы в этом контуре должны завершаться намного быстрее, чем во внешнем, поэтому зададим желаемое время переходного процесса на порядок быстрее, чем время выхода на экстремум:
![]()
Так как динамическая часть объекта линейная, то воспользуемся операторной процедурой модального метода синтеза.
Передаточная
функция объекта: 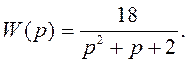
Корректор
статики: 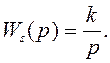
Корректор
динамики: 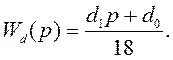
Действительное характеристическое уравнение:
![]()
Так как в системе допустимо перерегулирование (30%), то выберем 2 комплексно-сопряженных и один вещественный корень, исходя из требуемого быстродействия (0,2 с):
![]()
Желаемое характеристическое уравнение:
![]()
Приравнивая коэффициенты при соответствующих степенях p, находим параметры регулятора:
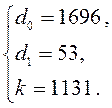
Для реализации корректора динамики рассчитаем стабилизирующую добавку L(p):
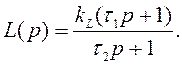
Характеристическое уравнение фильтра:
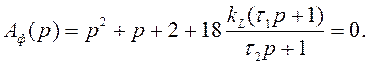
Так как переходные процессы в фильтре должны завершаться быстрее, чем процессы в объекте, зададим желаемое время процессов в фильтре:
![]()
Выберем вещественные корни:
![]()
Желаемое характеристическое уравнение фильтра:
![]()
Приравнивая коэффициенты при соответствующих степенях p, находим неизвестные параметры фильтра:
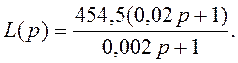
![]()
Внешний регулятор
Используем
интегральный закон управления: ![]()
Градиент:
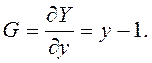
Параметр
![]() выбираем исходя из требуемого времени
выхода на экстремум:
выбираем исходя из требуемого времени
выхода на экстремум:
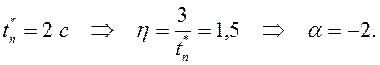
Градиент оценивается с помощью фильтра оценки частной производной, модель которого имеет вид:
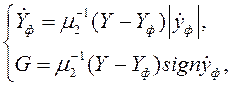
где
![]() – постоянная времени фильтра оценки
частной производной.
– постоянная времени фильтра оценки
частной производной.
Производная
![]() оценивается при помощи дифференцирующего
фильтра, передаточная функция которого имеет вид:
оценивается при помощи дифференцирующего
фильтра, передаточная функция которого имеет вид:
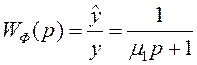 , где
, где
![]() – постоянная времени дифференцирующего
фильтра.
– постоянная времени дифференцирующего
фильтра.
С
учётом условия разделимости движений выбираем ![]() ,
, ![]() .
.
Результаты моделирования
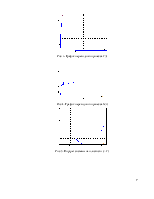
Структурная схема моделируемой системы приведена на рис. 1.
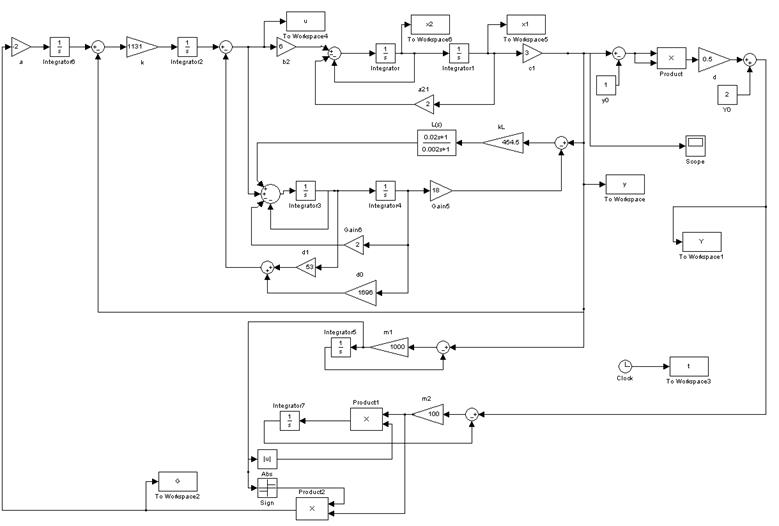
Рис. 1. Структурная схема системы
Результаты моделирования при начальных условиях x2(0) = 0, x1(0) = 1, y(0) = 3, Y(0) = 4 представлены на рис. 2-8.
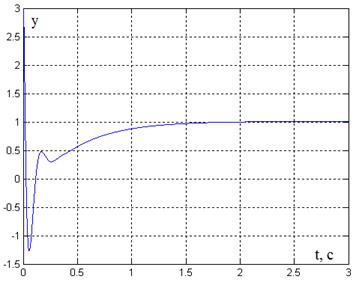
Рис. 2. График переходного процесса y(t)
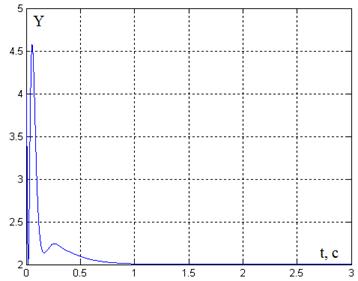
Рис. 3. График переходного процесса Y(t)
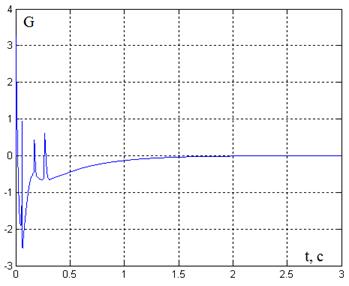
Рис. 4. График переходного процесса G(t)
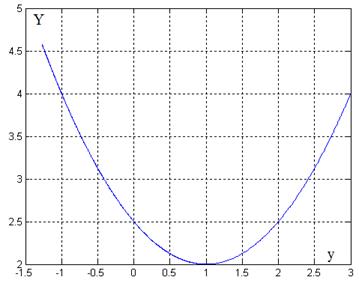
Рис. 5. Портрет системы на плоскости (y, Y)
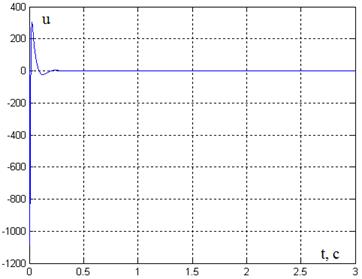
Рис. 6. График переходного процесса u(t)
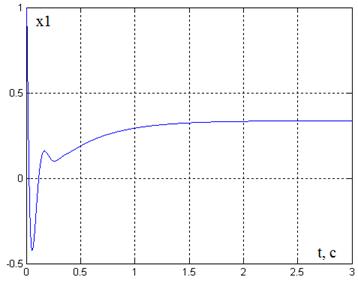
Рис. 7. График переходного процесса x1(t)
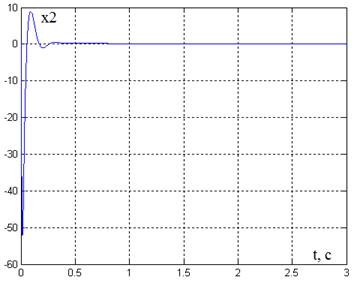
Рис. 8. График переходного процесса x2(t)
Выводы
Для заданного объекта управления была рассчитана и исследована система экстремального регулирования. Время выхода на экстремум составляет порядка 1,5 с. Ресурс управления не превышен.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.