Синтез одноканальных систем. Компенсатор и предкомпенсатор, уравнение в псевдосостояниях, собственные значения, желаемая область, u-устойчивость, робастная асимптотическая достижимость, страница 2

S124.  Рассмотрим систему с компенсатором:

Система (обозначим ее ) состоит из объекта и компенсатора с двумя входами:  - передаточная функция по входу ,  - передаточная функция по входу . В данной системе  - вход,  - выход,  - возмущения,  - выход компенсатора. У компенсатора два входа и один выход. Объект описывается передаточной функцией . Задача следующая: выбрать компенсатор такой, чтобы он был правильным, система  была устойчивой. Переходный процесс  был хорошим. Возможно наложение дополнительных условий.

Принято называть  предкомпенсатором (precompensator) и  компенсатором в обратной связи (feedback compensator). Полином  называют общим знаменателем (common denominator).

Дополнительные условия:  - взаимно простые полиномы, . Объект описывается уравнениями

.

Кратко это можно записать так: .

Компенсатор можно записать в виде блочной матрицы:

.

Здесь . В уравнениях компенсатор записывается так:

                          .                    (а)

Кратко это записывается так: .

S125.  Перейдем к матричному описанию системы :

  

С учетом этих обозначений систему  можно описать уравнением:

                                                  (а)

Это уравнение называют уравнением в псевдосостояниях (pseudo-state equation) и обозначают . Матрицы  и  имеют вид

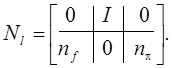                                       (б)

Уравнение  в виде полиномиального матричного разложения можно записать стандартным образом:

                             (в)

Второе уравнение равносильно . Матрицы таковы:

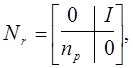
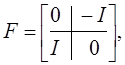
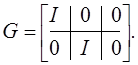                                  (г)

$31.  Показать, что уравнение (а) из S125, где матрицы  и , заданные в (б) S125, соответствуют уравнениям (а) из S124.

У к а з а н и е. Подставим (б) S125 в (а) S125:

 

Учтем, что : . Так как , получим (а) из S124.

$32.  Показать справедливость формул (в) и (г) из S125.

У к а з а н и е. Вспомнив обозначения векторов S125, подставим (г) из S125 в (в) из S125:

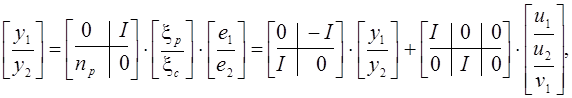
что соответствует уравнениям:

 

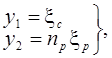
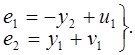
S126.  Из первого уравнения (в) S125 и уравнения (а) S125

                                     (а)

получим передаточную функцию :

, где . Систему (а) будем кратко обозначать  .

Выпишем второе уравнение из (в) S125 и (а) из S125:

, .                           (б)

Найдем передаточную функцию :

, где . Систему (б) кратко обозначаем  .

$33.  Покажите, что

, .

Здесь использовано равенство .

S127.  У системы  (см.S124) ,  – хорошо устроены. Чтобы доказать это, необходимо доказать правильность , , , . Например, покажем, что  – правильная передаточная функция:

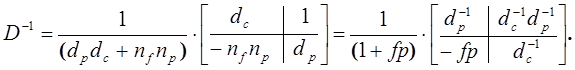
Но  – правильное и элементы последней матрицы правильные. Следовательно,  – правильное.

S128.  Уточним терминологию для системы : вектор  называют вектором псевдосостояния системы (pseudo-state); характеристическим полиномом  (characteristic polynomial) называют полином

;

собственным значением  (eigenvalue) называют корень . Система  называется экспоненциально устойчивой, если  – экспоненциально устойчивая.

При синтезе предпочитают располагать собственные значения системы в левой полуплоскости комплексной плоскости, а в некоторых случаях размещают их в заданной области левой полуплоскости. Область, в которой нежелательно размещать собственные значения, называют нежелаемой областью (undesirable) и обозначают и. Нежелаемая область – замкнутая и . Желаемая область (desirable) обозначается . Систему  называют и-устойчивой (и-stable), если D_g хорошо устроена и собственные значения замкнутой системы расположены в .