Задача синтеза непрерывных адаптивных систем с моделью

То, что мы знаем, -  ограничено, а то,

чего мы не знаем, - бесконечно. (П.С. Лаплас)

2. ЗАДАЧА СИНТЕЗА НЕПРЕРЫВНЫХ АДАПТИВНЫХ СИСТЕМ с моделью

2.1 Постановка задачи адаптивного управления

Рассмотрим класс нелинейных динамических систем, которые  описываются уравнениями состояния вида

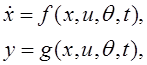                                                (2.1)

где хÎRⁿ , yÎR^l , uÎR^m , θÎR^s - векторы переменных состояния, выходных переменных, управляющих воздействий, параметрических возмущений соответственно  (рис. 2.1). Уравнение (2.1) может описывать объект управления вместе с  исполнительным и измерительным устройствами. Вектор – функции  f, g предполагаются известными, гладкими с ограниченными частными производными,

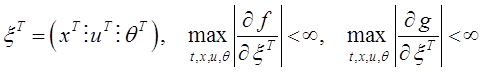, матрица частных производных 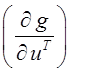должна быть невырожденной. Зависимость f , g от θ и времени t отражает неопределённость математической модели и характеристик внешней среды. В реальных условиях параметрические и аддитивные возмущения ограничены. В некоторых случаях верхние оценки уровня и темпа изменения возмущений:

                             (2.2)

считаются известными.

Полагаем, что желаемое поведение системы задано эталонной моделью вида

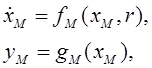                                             (2.4)

где x_мÎRⁿ – вектор переменных состояния модели, y_мÎR^l – вектор выходных переменных модели,   - вектор эталонных входных воздействий. Близость характеристик системы и эталонной модели оценим с помощью положительной функции Q. Тогда цель управления зададим в виде неравенства

,                                        (2.3)

где δ_q – допустимое минимальное значение функции Q , которую будем называть целевой функцией.

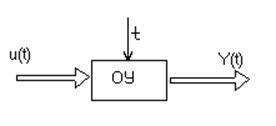
Рис. 2.1.

Задача синтеза адаптивной системы управления состоит в определении алгоритма управления

                                                                                 (2.5)

и алгоритма адаптации

                                                                                 (2.6)

которые обеспечивают достижение поставленной цели (2.3) в системе (2.1), (2.4)-(2.6) для любых возмущений из ограниченного множества ().  Для элементов ограниченной области W_q справедливо неравенство (2.2). В уравнениях (2.5), (2.6)  u_t,  k_t – некоторые операторы.

Система (2.1), (2.4) - (2.6) называется адаптивной в классе W_q по отношению к цели (2.3), если для любого qÎW_qи при любых начальных условиях x(0), u(0), k(0) из заданного множества выполняется условие (2.3).

2.2 Этапы синтеза адаптивной системы

Согласно (2.5), (2.6) адаптивные системы содержат контур, формирующий управление (u) и контур, в котором вырабатываются текущие значения коэффициентов регулятора. Поэтому говорят о двухуровневой структуре адаптивных систем. Подобно любой системе автоматического управления синтез адаптивной системы состоит из общих  этапов расчета  и этапов, обусловленных двухуровневой структурой:

1.  Определение математической модели объекта управления,

2.  Проверка устойчивости, управляемости, наблюдаемости по линеаризованной модели исходного квазистационарного объекта,

3.  Определение граничных условий (2.2), начальным условий в объекте, а также ресурсных  ограничений  по управлению,

4.  Определение целевой функции (Q),

5.  Синтез основного контура (2.5),

6.  Синтез контура адаптации (2.6),

7.  Проверка устойчивости замкнутой системы.

К этапам, обусловленным двухуровневой структурой системы, относятся синтез основного контура (2.5) и синтез контура адаптации (2.6). Среди существующих методов проектирования регуляторов можно выделить следующие:

1)  метод эталонного уравнения (или метод инвариантности). Уравнение закона управления получается из равенства правых частей уравнений эталонной модели и модели объекта управления, разрешенных относительно  старших производных выходных переменных или координат состояния;

2)  модальный метод; для определения закона управления используется желаемое расположение собственных чисел матрицы системы;

3)  методы оптимального управления. Закон управления получается в результате решения задачи оптимизации по управляющему воздействию некоторого обобщённого показателя качества;

4)  метод сингулярных возмущений; синтез закона управления выполняется по упрощенной модели системы, которая получается в результате выделения подсистем быстрых и медленных процессов. Закон управления определяется по модели, описывающей подсистему медленных движений. 

Кроме того, структура основного контура может быть задана одним из типовых законов управления: пропорциональным, пропорционально - интегральным, пропорционально – дифференциальным или пропорционально – интегрально – дифференциальным.

В результате применения одного из перечисленных методов получают «идеальный» закон управления . Выполнив замену неизвестных возмущений настраиваемыми коэффициентами, приходят к реальному закону управления , который в частном случае может описываться  линейным уравнением

где k_х,, k_r – матрицы настраиваемых коэффициентов соответствующих размерностей.

Далее определяется вид оператора k_t  (2.6). В системах прямого адаптивного управления алгоритм настройки коэффициентов регулятора