Рекомендации к разработке модели водонагревателя. О реализации обратной связи. Рекомендации к проведению синтеза регулятора с использованием приемов оптимизации. Функция желательности Харингтона, страница 7

3. В вершинах симплекса сравниваются показатели качества (отклики), выбирается вершина с минимальным откликом и отражается относительно противолежащей грани. Находится вершина следующего симплекса, k вершин которого одновременно являются и вершинами предыдущего симплекса. Координаты отраженной вершины вычисляют по формуле:

,                                 (4)

где- j-я координата наихудшей точки l; - j-я координата новой точки, получаемой в результате отражения; - j-я координата центра противоположной грани

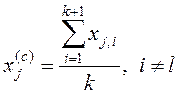.                                                (5)

Если минимальный отклик оказался сразу в двух вершинах, то вопрос, какую из них отражать, решается произвольно.

4. Выполняется вычислительный эксперимент в отраженной вершине нового симплекса, и отклик в ней сравнивают с откликами в остальных вершинах, а затем снова выбирают вершину с минимальным откликом по правилу п.3. Если в новой вершине  (k + 1)-го симплекса оказался опять минимальным, то возвращаются к k-му симплексу, и отражают вторую по минимальности вершину. Если это явление повториться, то отражают третью по минимальности вершину и т.д.

5. Эксперимент продолжают до тех пор, пока симплекс не совершит полный оборот вокруг одной из вершин. Как уже отмечено выше, точность нахождения точки экстремума зависит от размера симплекса. Для уточнения положения экстремальной точки в последних симплексах рекомендуется уменьшить длину стороны t, а также выполнить опыт в середине симплекса (условное название практически экстремальной точки - S), в вершинах которого отклик оказался максимальным по сравнению с остальными симплексами (имеется ввиду состояние до зацикливания).

Координаты точки S определяются по условию:

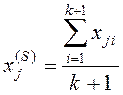 .                                                               (6)

Эти координаты позволяют определить практически экстремальное значение обобщенного показателя качества D, а также оценить коэффициенты чувствительности к разбросу варьируемых параметров в точке экстремума по формуле:

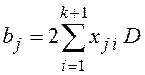.                                                         (7)

Если необходимо для представления интерполяционной математической модели (получить полином, описывающий поведение анализируемого показателя качества вблизи экстремума), то можно рассчитать и свободный член полинома:

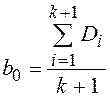.                                                                (8)

К достоинствам симплексного метода относится: достаточно высокая помехоустойчивость при выборе направления движения к экстремуму; сочетание изучения поверхности отклика с одновременным рабочим движением к экстремуму; обеспечение высокой скорости выхода к области экстремума; высокая оперативность. Метод не предъявляет жестких требований к аппроксимации поверхности отклика плоскостью. Исходный k-мерный симплекс можно достроить до (k+1) – мерного симплекса, вводя только одну новую точку (для других планов это удваивает число опытов). Тогда все точки k-мерного симплекса в действительности представляют собой точки (k + 1)-мерного пространства, которые находятся в гиперплоскости , где с_s− фиксированное значение (k+1)-го фактора в безразмерном виде. Для построения симплекса размерностью (k+l) из k-мерного симплекса необходимо найти центр тяжести точек k-мерного симплекса в (k+1)-мерном пространстве и провести через эту точку перпендикуляр к гиперплоскости, в которой лежат точки k - мерного симплекса. Отложив на этом перпендикуляре отрезок длиной h_k+1 (высота k+1 - мерного симплекса), можно получить точку, которая вместе с исходными данными образует (k+1)-мерный симплекс. Координаты новой точки:

,                                (9)

где - j - ая координата центра исходного симплекса, - высота симплекса, найденная по условию

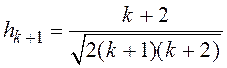.                                              (10)