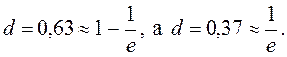Рекомендации к разработке модели водонагревателя. О реализации обратной связи. Рекомендации к проведению синтеза регулятора с использованием приемов оптимизации. Функция желательности Харингтона, страница 5

                                                      (2)

Шкала d является безразмерной. Она позволяет любое физическое свойство преобразовать так, чтобы его можно было интерпретировать в терминах полезности или желательности для специфического применения.

Простейшим типом преобразования служит такое, в котором существует не допускающий изменения верхний и (или) нижний пределы спецификации свойства. Частная функция желательности при одностороннем ограничении (рис.1, а) имеет вид

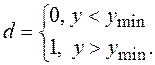                                                                               (3)

Аналогичным образом получается частная функция желательности, если спецификация задает ограничение сверху. Если для данного свойства существует двустороннее ограничение, то (рис.1, б)

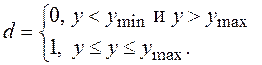                                                           (4)

Представленными условиями при решении оптимизационных задач пользуются, например, при назначении ограничений конструктивных размеров. Однако при оценке свойств объектов проектирования практически всегда желательно, чтобы значение свойства находилось не только между пределами спецификации, но и на определенном расстоянии от них. Это необходимо, например, чтобы противостоять присущим производственному процессу случайным колебаниям. Кроме того, довольно трудно бывает провести точную пограничную линию между приемлемым и неприемлемым значением свойства. Поэтому в общем случае преобразование y и d осуществляется по более сложным законам. Для двустороннего ограничения вида y_minyy_maxпреобразование y в d рис.3 производится при помощи выражения

                                                              (5)

где n - положительное число (n>0), не обязательно целое;

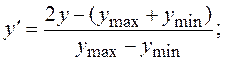                                                 (6) показатель степени n можно вычислить, если поставить в соответствие значению yзначение d(предпочтительно в интервале 0.6 < d < 0,9) по формуле

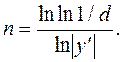                                                                    (7)

Задавая при помощи контрольной точки крутизну кривой желательности, можно учесть особую важность отдельных свойств; для них nбудет иметь большее значение, и малому значению свойства вблизи ограничивающих пределов будет соответствовать резкое изменение желательности. Величина n определяет наклон кривой. Когда nстановится большим, кривая приближается к своей предельной форме (см. рис.3). Если нет спецификации, целесообразно дать статистическую оценку n по ряду значений y и соответствующих d.

Для односторонних ограничений вида или более удобной формой преобразования y в d служит экспоненциальная зависимость (рис.2):

                                                         (8)

В выражении (8) . Коэффициенты b₀и b₁ можно определить, если задать для двух значений свойства y соответствующие значений желательности d предпочтительно в интервале 0,2 < d< 0,8. Нелинейное преобразование yв y' применяется, если данное свойство имеет особую важность, нарушение ограничивающих условий недопустимо и малому изменению свойства вблизи ограничивающего предела соответствует резкое изменение желательности. Одностороннее ограничение наиболее часто встречается на практике.

Имея несколько свойств, преобразованных в шкалу d, можно обобщенную функцию желательности находить в виде среднего геометрического частных функций желательности согласно (1). При выполнении курсовой работы выбираемыми свойствами, по меньшей мере, могут быть взяты: перерегулирование и потребляемая на парирование возмущения энергия. Для учета потребительских свойств целесообразно включить в число свойств и время переходного процесса. Необходимо весьма ответственно подходить к оценке свойств по частным шкалам желательности (не обольщаться в возможности достигнуть очень хороших оценок, понимать роль ограничений и их наличие по физическому смыслу).