Рекомендации к разработке модели водонагревателя. О реализации обратной связи. Рекомендации к проведению синтеза регулятора с использованием приемов оптимизации. Функция желательности Харингтона, страница 6

Поиск экстремума с целью определения параметров регулятора МЕТОДОМ СИМПЛЕКС-ПЛАНИРОВАНИЯ

(нумерация формул в пределах раздела)

Изложение выполнено применительно к вычислительному эксперименту для итерационной настройки параметров регулятора.

Весьма удобным для параметрического синтеза устройств и систем автоматики представляется использование симплекс-планирования. Развитие этого метода известно как метод деформируемого многогранника или метод Нелдера-Мида. Примеры его использования можно найти в демонстрационных программах Simulink (Blocsets &Toolboxes/NCD Blocset/например, ncd demo3).

Для выполнения курсовой работы достаточно решать задачу выбора параметров настройки регулятора путем целенаправленного перебора вариантов, проводя вычислительный эксперимент и руководствуясь изложенными ниже определениями и положениями симплекс-планирования.

Симплексом называют многогранник, имеющий k+1 вершину в пространстве k факторов, каждая из которых определяется пересечением k гиперплоскостей данного пространства. В пространстве одного фактора (k = 1) симплексом служит отрезок установленного размера, при k = 2 – треугольник, при k = 3 – тетраэдр.

Метод позволяет совмещать пробные опыты для определения направления движения с рабочим движением по поверхности отклика к области оптимума. Основная идея метода заключается в том, что проводятся опыты во всех k + 1 вершинах симплекса и по величине отклика в них определяется направление движения к экстремуму.

При планировании вычислительных экспериментов используются регулярные симплексы (расстояния между всеми его вершинами равны). Однако регулярность симплекса и свойство ротатабельности планов (при работе со случайными величинами – оценка результатов с одинаковым рассеянием) не будут инвариантными к масштабу координат факторного пространства. Это не отвечает условиям поиска области экстремума с надлежащей точностью. При изменении масштаба регулярный симплекс может стать нерегулярным. Чтобы сделать симплекс регулярным, используется линейное преобразование:

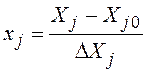,                                                      (1)

где − j-я координата центра плана (начальное значение варьируемого параметра,  j = 1, 2, …, k); − интервал варьирования по j-му параметру; X_j – абсолютное значение варьируемого параметра.

Метод последовательного симплекс-планирования характеризуется следующей последовательностью действий.

1. Для всех варьируемых параметров выбираются начальные значения   и  интервалы их варьирования . От выбора этих величин зависит качество и длительность поиска, поэтому решение принимается на компромиссной основе и априорных представлениях о поверхности отклика. Существенное значение имеет исходное значение вектора (близость к области экстремума). Для выбора интервала варьирования реально можно исходить из . В области экстремума величину интервала можно уменьшить, изменив в плане эксперимента размер грани симплекса.

2. Вычисляются координаты вершин начального симплекса. При совмещении центра симплекса с началом координат и размещении одной из вершин на координатной оси план эксперимента для k факторов состоит из k столбцов и k+1 строк:

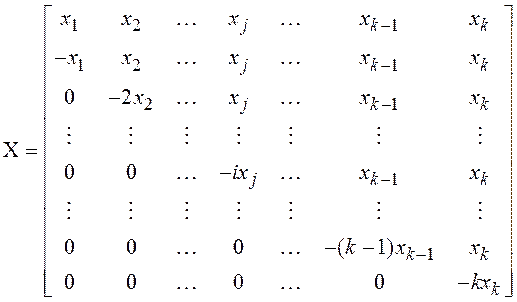.               (2)

Кодированные значения факторов принимают значения:

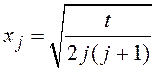,                                                    (3)

где  t - длина стороны симплекса (за исходное значение следует принимать t = 1, при необходимости более точного поиска в области экстремума по мере приближения к нему можно принять t < 1).

Для практического использования матрицы (2) по формуле (3) подсчитаны и ниже приведены числовые значения её элементов, линиями выделен план для k=5:

.

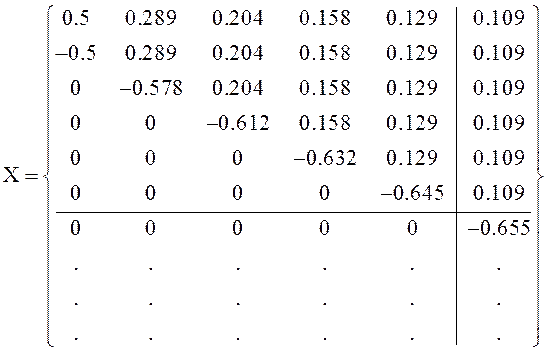Последующие действия на примере k = 2 иллюстрирует приведенный рисунок.