Режим реактивной мощности, как физический процесс, тесно связан с перепадом напряжений линии электропередачи.
Перепадом напряжений, обычно, называют отношение величин напряжений начала и конца линии:
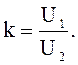
В параграфе 4.4 были рассмотрены различные режимы реактивной мощности электропередачи.
Обычные линии электропередачи работают с отстающим коэффициентом мощности, т.е. вместе с активной мощностью передается определенное значение реактивной мощности. Это значение определяется допустимым перепадом напряжений и экономическими соображениями. Для линий различных номинальных напряжений допускаются следующие перепады напряжений: для Uном £ 220 кВ – k £ 1,15; для Uном = 330 кВ – k = 1,1 и для Uном ³ 500 кВ – k = 1,05.
Для протяженных линий передача реактивной мощности связана с большим перепадом напряжений, что иллюстрирует векторная диаграмма, изображенная на рис. 7.25. Диаграмма построена для линии без потерь по уравнениям (7.5) при следующим данных: Р = 150. МВт; l = 1000 км; Uном = 220 кВ; Zв = 400 Ом; cosj = 0,8 (пунктир) и cosj2 = 1 (сплошные линии).
Из векторной диаграммы следует, что при отстающем коэффициенте мощности в линии получается очень большой перепад напряжений (k = 1,6). При cosj2 = 1 перепад напряжений будет небольшой (k = 1,13).
При опережающем токе I2 ЭДС генераторов передающей станции уменьшается по сравнению с этой ЭДС при cosj = 1, что отрицательно действует, как это видно из выражения (7.18), на системы передачи. Поэтому работа с опережающим коэффициентом мощности нежелательна.
Проверим эти предварительные соображения, найдем выражения реактивной мощности в начале и конце линии и проведем анализ ее различных режимов, установим ее зависимость от перепада напряжений.
Для общности решения будем представлять линию и ее участки четырехполюсниками.
Тогда фазовое напряжение в любой точке линии представится выражением
где Аn и Вn –
эквивалентные постоянные участка линии от ее конца до рассматриваемой точки n.
Зависимости эквивалентных сопротивлений линии от длины [39] показывают, что при длинах l £ 2700 км активные сопротивления не оказывают существенного влияния на эквивалентные сопротивления линии и системы передачи, поэтому для исследования вопросов пропускной способности, перенапряжений, токов коротких замыканий, режимов реактивной мощности, возможно рассматривать вместо реальной линии – линию без потерь и упомянутое напряжение в любой точке линии записать в виде
Здесь U2ф принято за ось отсчета и учтено, что в уравнениях четырехполюсника без учета потерь обобщенные постоянные А и D представляют собой чисто вещественные числа, а В и С – чисто мнимые.
Подставляя в выражение для Unф ток I2 через мощности и переходя к относительным единицам на базе натуральной мощности (Рбаз = Рнат), получим
(7.19)
где удельные мощности в конце линии
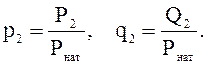
Модуль напряжения
(7.20)
или, вводя модуль полной мощности в конце линии,
(7.21)
Формула (7.19) дает возможность определить напряжение в любой точке электропередачи по данным конца линии. Аналогичным путем нетрудно получить значение напряжения в любой точке линии по данным начала в виде
(7.22)
Величина напряжения
(7.23)
или
(7.24)
Для определения реактивной мощности q1 запишем по выражению (7.22) напряжение U2ф
где Ал, Dл, Вл и Сл – обобщенные
постоянные всей линии.
Из этого выражения получим
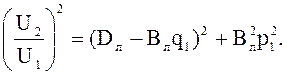(7.25)
Согласно формуле (7.17) передаваемую активную мощность можно представить в виде
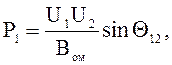где Вом – обобщенная постоянная определяет эквивалентное
сопротивление линии в омах.
Переходя к относительным единицам, получим
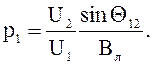(7.26)
Подставляя это значение в выражение (7.25), получим
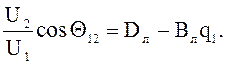
Отсюда найдем
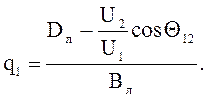(7.27)
При работе без перепада напряжений вместо формул (7.26) и (7.27) получим
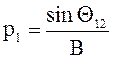(7.24)
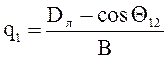(7.25)
и для однородной линии*
передачи при работе с перепадом напряжений
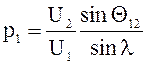(7.26)
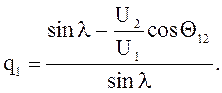(7.27)
При работе однородной линии без перепада напряжений
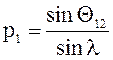, (7.28)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.