Более удобной для линии передачи оказывается П‑образная схема замещения. Для примера найдем значения обобщенных постоянных П‑образной схемы замещения.
Для холостого хода:
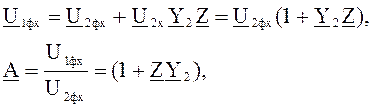
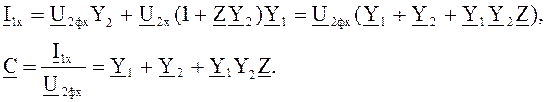
Для короткого замыкания:
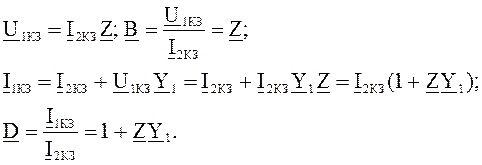
Можно решать обратную задачу: при известных А, В, С, и D определить Y1, Y2 и Z:
.
Отсюда
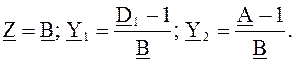
При расчете линии передачи при помощи схемы замещения прежде всего подсчитываются ее параметры, так, например, для схемы П ‑ Y1, Y2 и Z.
Для воздушных линий до 300 км постоянные Z, Y1 и Y2 можно подсчитать без учета равномерности распределения постоянных линии, т.е. по формулам:
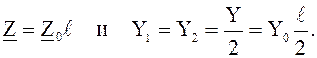
Для линий более 300 км для учета равномерности распределения постоянных необходимо действительные постоянные линии и Y умножить на поправочные коэффициенты kZ и kY. Таким образом сопротивление и проводимость П‑образной схемы замещения будут
Коэффициенты kZ и kY можно определить из уравнений:
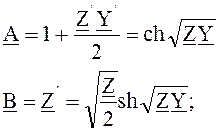из второго уравнения находим:
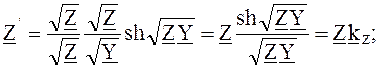из первого и второго уравнений можно найти:
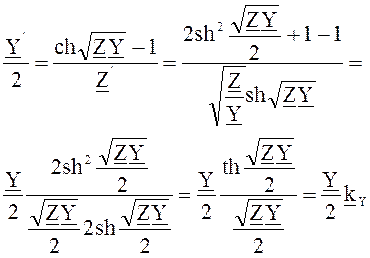
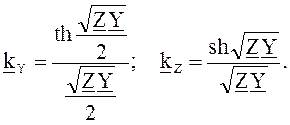
При расчете электропередачи возможны две задачи: или по заданным напряжению U2, току I2 и коэффициенту мощности cosj2 на шинах понизительной подстанции требуется найти напряжение U1 и ток I1 и коэффициент мощности cosj1, на шинах электростанции (рис. 7.3), или наоборот, по заданным U1, I1, cosj1, найти U2, I2, cosj2. Решение второй задачи аналогичной решению первой, причем чаще встречается первая. Поэтому различные методы электрического расчета рассмотрим применительно к первой задаче.
а) Графический метод.
Электропередача, состоящая из повысительной подстанции, линии высокого напряжения и понизительной подстанции, может быть схематически представлена рис. 7.3,а.
Полная схема замещения этой электропередачи с принятием для линии П‑образной схемы, для трансформаторов Т‑образных схем изображена на рис. 7.3,б.
Для определения U1, I1 и cosj1 строим векторную диаграмму (рис. 7.4). Величины векторов падений напряжений и токов определяются из выражений:
1) 
2) 
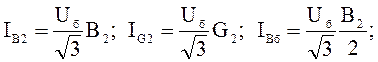
3) 
4) 
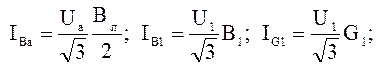
5) 
Мощность в начале электропередачи:
Коэффициент полезного действия:
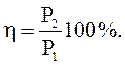
Потери мощности в линии и трансформаторах
DР = Р1 – Р2 или в процентах к мощности, отпускаемой с шин понижающей подстанции,
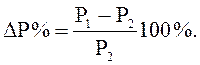
Потери напряжения в линии
U = U1 – U2 или в процентах:
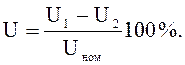
В случае обратной задачи, когда заданы величины U1, I1, cosj1 и нужно найти U2, I2, и cosj2, построение векторной диаграммы ведется в обратном порядке и вместо сложения производится вычитание векторов падения напряжения и токов утечки.
б) Аналитический метод.
Определим напряжение точки б (рис. 7.3):
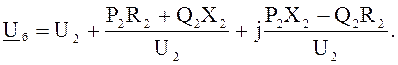
Находим потери мощности в трансформаторах понизительной подстанции:
1) в сопротивлении R2
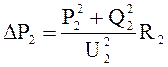или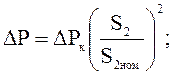 
2) в сопротивлении Х2
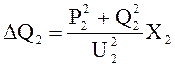или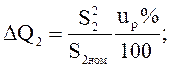 
3) в проводимости G2 ‑ DР2х, даются заводом;
4) в проводимости B2
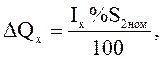так
как 
5)
в проводимости 
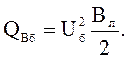
Мощность в конце участка R, X:
Определяем напряжение в точке а:
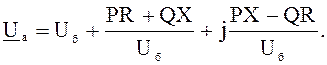
Емкостная мощность в точке а:
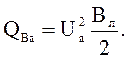
Потери мощности на участке аб:
1) в активном сопротивлении R:
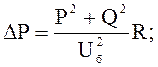
2) в индуктивном сопротивлении Х:
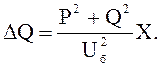
Мощность в конце участка R1 X1:
Вычисляем напряжение в начале электропередачи:
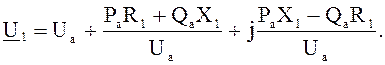
Потери мощности на участке I a:
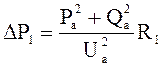и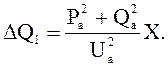 
Мощность в начале электропередачи:
Векторная диаграмма, соответствующая проделанному расчету, изображена на рис. 7.5.
в) Метод обобщенных постоянных.
Каждый элемент электропередачи (трансформаторы и линию) можно рассматривать как четырехполюсник и написать для каждого из них уравнения четырехполюсника. Рассматривая всю электропередачу также как четырехполюсник, выразим обобщенные постоянные электропередачи через обобщенные постоянные ее элементов.
Предварительно найдем обобщенные постоянные двух эквивалентных элементов (рис. 7.6), соединенных последовательно.
Для этих элементов можно написать уравнения:
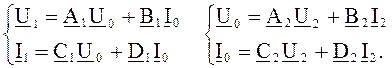
Подставляя вторую систему в первую, после преобразований получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.