Общая характеристика электропередач и порядок их электрического расчета. Круговые диаграммы электропередачи. Угловые характеристики мощности и предельная передаваемая мощность, страница 2

b ‑ коэффициент затухания колебаний на единицу длины;

a ‑ коэффициент изменения фазы.

Введя гиперболические функции

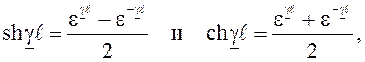выражения (7.2), (7.3) можно переписать

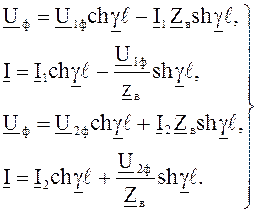                              (7.4)

Для b, a, R_в и Х_в(Z_в=R+jx_в) можно получить следующие выражения:

                           

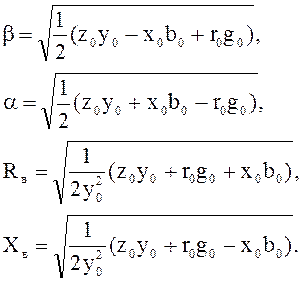
Если пренебречь потерями в линии, полагая r₀ = 0 и g₀ = 0, то

                                      

                                                Z_в = R_в и для так называемой линии без потерь вместо (7.4) получим:

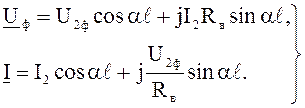                                                      (7.5)

Величина  называется волновой длиной линии.

Процессы в линиях передачи имеют волновой характер и, исходя из выражений (7.2), напряжение в любой точке линии можно представить, как результат сложения падающей волны

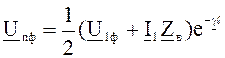                                                                    (7.6) и отраженной

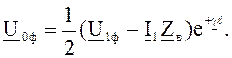                                                                  (7.7)

Аналогично для тока

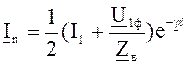                                                                          (7.8)

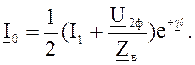                                                                        (7.9)

Длина волны

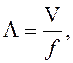                                               где V = w/a ‑ фазовая скорость для линии без потерь совпадает со скоростью распространения электромагнитной энергии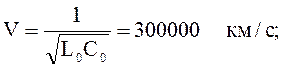                                        

f – частота приложенного напряжения.

При f = 50 пер./с L ‑ 6000 км.

Волновую длину линии можно выразить

                                               

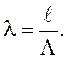
Для воздушной линии волновая длина в градусах

                                      

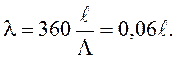
Если на приемном конце линии имеет место соотношение

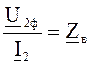                                             , т.е. линия включена на волновое сопротивление, тогда, как видно из выражений (7.7) и (7.9), отраженной волны не будет, и уравнения (7.3) можно записать в виде:

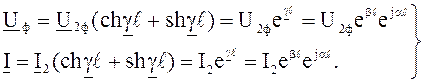                                (7.10)

Напряжение и ток изменяются совершенно одинаково: абсолютные величины – по экспоненциальному закону, который характеризуется коэффициентом e^bl и изменение фазы определяется коэффициентом е ^jal.

Такой режим, при котором сопротивление приемника равно волновому сопротивлению линии, называется натуральным.

Для линии без потерь при натуральном режиме уравнения (7.10) будут иметь вид:

                                   

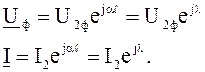
Таким образом, натуральный режим для линии без потерь характеризуется постоянством абсолютных значений напряжения и тока и изменением лишь фазы, которое равно волновой длине линии, выраженной в единицах угловых величин. Мощность, соответствующая натуральному режиму,

                                 

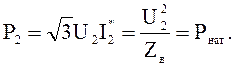
Эта мощность называется натуральной или естественной. Мощность линии, выраженная в долях от натуральной, называется удельной нагрузкой линии или удельной мощностью.

                                        

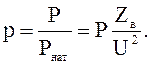
Если сопротивления приемника Z_n отличается от волнового сопротивления Z_в, то помимо падающей волны, которая для напряжения  и тока соответственно выражается формулами (7.6) и (7.8), будет существовать отраженная волна, которая определяется формулами (7.7) и (7.9). Отраженная волна дополнительно нагружает провода линии передачи и создает дополнительные потери энергии и повышения напряжения.

Линия передачи представляет собой четырехполюсник, для которого можно написать уравнение:

                                      U_1ф = А U_2ф + В I₂

                                       I₁ = C U_2ф + D I₂, где А, В, С, и D – эквивалентные или обобщенные постоянные четырехполюсника, причем

               

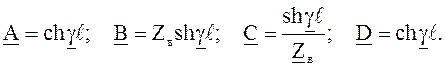
Вследствие симметрии линии относительно своих концов А = D. Для обычно встречающихся схем пассивного четырехполюсника, справедливо соотношение:

                                         А D – В С = 1.

Рассматривая режимы холостого хода (х.х.) и короткого замыкания (КЗ), получим:

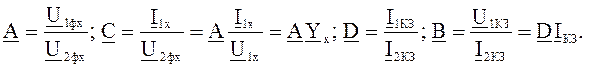
Постоянные А и D отвлеченные числа. С – равна проводимости холостого хода в начале схемы, умноженной на коэффициент А, т.е. С имеет размерность проводимости. В – равно полному сопротивлению короткого замыкания в конце схемы, умноженному на коэффициент D, т.е. В имеет размерность сопротивления.

Всякий четырехполюсник может быть замещен П или Т‑образной схемой замещения с сосредоточенными постоянными (рис. 7.2).