Исследование простой нелинейной цепи переменного тока (Лабораторная работа № 25Н)

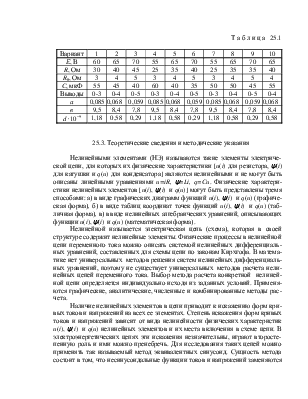
темы нелинейных алгебраических уравнений может быть выполнено методом последовательных приближений (вручную или на ЭВМ  по программе «Given…Find»).

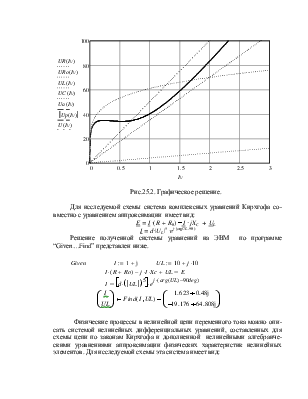
Рис.25.2. Графическое решение.

Для исследуемой схемы система комплексных уравнений Кирхгофа совместно с уравнением аппроксимации  имеет вид:

E = I ·(R + R₀) - I · jX_С  + U_L

I = d·|U_L|⁵ ·e^{j∙(argUL-90)}

Решение полученной системы уравнений на ЭВМ  по программе “Given…Find” представлен ниже.

Физические процессы в нелинейной цепи переменного тока можно описать системой нелинейных дифференциальных уравнений, составленных для схемы цепи по законам Кирхгофа и дополненной  нелинейными алгебраическими уравнениями аппроксимации физических характеристик нелинейных элементов. Для исследуемой схемы эта система имеет вид:

i ·R+ i·R₀++ u_С= e(t );(1)

i = C·;(2)

i= a·sinh(b·y).                                   (3)

Приводим систему дифференциальных уравнений к стандартной форме (Коши). Для этого cделаем подстановку (3) в (1) и (2) и выразим производные:

= (R+·R₀) · a·sinh(b·y) − u_С + e(t );

= (1/C) · a·sinh(b·y)

Решение системы уравнений Коши может быть выполнено методом численного интегрирования (численным методом) на ЭВМ  по стандартной программе rkfixed (метод Рунге-Кутта 4-го порядка с фиксированным шагом интегрирования:

Результатом решения являются массивы значений (матрицы) переменных величин. Действующие значения токов и напряжений определяются через массивы значений соответствующих функций по формулам:

Найденные методом численного интегрирования действующие значения токов и напряжений могут существенно отличаться (на 10-20%) от аналогичных значений, определенных методом эквивалентных синусоид.

При выполнении экспериментальных измерений можно с достаточной степенью точности считать U_К = U_L , так как активная составляющая этого напряжения относительно мала.

25.4. Расчетная часть

1. По уравнению аппроксимации вольт-амперной характеристики I_L(U)= d·U⁵ определить координаты 8 точек в интервале значений тока I=0,5-2,0A согласно заданию. Результаты расчета внести в табл. 25.2.

2. В выбранных масштабах для напряжения m_U и для тока m_I построить в одной системе координат графические диаграммы вольт-амперных характеристик всех элементов схемы: U_L , U_R , U_Ro , U_C = f(I). Выполнить графическое сложение вольт-амперных характеристик отдельных  элементов схемы согласно уравнению 2-го закона Кирхгофа в векторной форме  и получить таким образом графическую диаграмму входной вольт-амперной характеристики E=f(I).

3. По графической диаграмме E=f(I) определить координаты 8 точек в интервале значений тока I=0,5-2,0A согласно заданию. Результаты графического расчета внести в табл. 25.3.

4. На графической диаграмме определить точку резонансного режима и соответствующее этой точке значение ЭДС источника Е_р.

5. По графической диаграмме п.2 выполнить расчет схемы для двух  значений ЭДС (заданного  Е и расчетного Е_р). Определить ток I и напряжения на отдельных элементах схемы U_R , U_K , U_C.. Результаты графического расчета внести в табл. 25.4 и 25.5.

6. Выполнить расчет исследуемой схемы путем решения нелинейного комплексного уравнения 2-го закона Кирхгофа по программе «Given…Find». Для двух  значений ЭДС (заданного  Е и расчетного Е_р)  определить