Исследование параллельной резонансной цепи (Лабораторная работа № 8Н)

Министерство образования Республики Беларусь

Кафедра “Электротехника и электроника”

Лабораторная работа по ТОЭ №8Н

ИССЛЕДОВАНИЕ ПАРАЛЛЕЛЬНОЙ РЕЗОНАНСНОЙ ЦЕПИ

М и н с к    2 0 10

Л а б о р а т о р н а я   р а б о т а   № 8Н

ИССЛЕДОВАНИЕ ПАРАЛЛЕЛЬНОЙ РЕЗОНАНСНОЙ ЦЕПИ

8.1. Цель работы

1. Исследование резонансных свойств параллельного колебательного контура.

2. Построение резонансных характеристик и векторных диаграмм напряжений и токов для параллельного колебательного контура.

8.2. Исходные данные

Заданы:

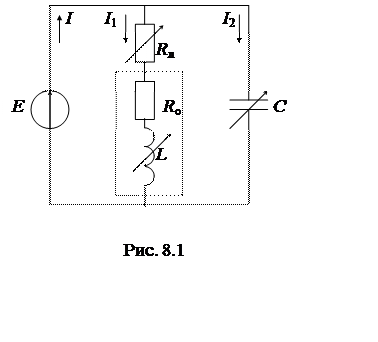
1. Эквивалентная схема исследуемой цепи (рис. 8.1). В схеме действует источник синусоидальной ЭДС с постоянной частотой  f= 50Гц.

2. Параметры элементов схемы (табл. 8.1), эквивалентное активное сопротивление R₁ = R_o + R_д, где R_o = 0,07∙Х_L - внутреннее активное сопротивление катушки.

3. Рабочая схема исследуемой цепи и схемы включения измерительных приборов (рис. 8.3).

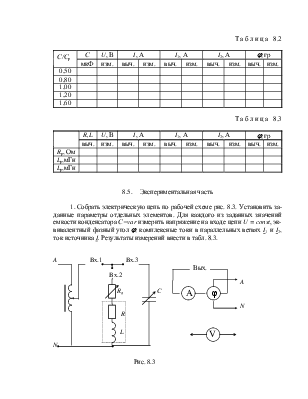
Т а б л и ц а   8.1

8.3. Теоретические сведения и методические указания

В электрической цепи, содержащей накопители энергии разного рода, в свободном состоянии возможны колебания энергии между магнитным полем  катушки W_м = Li²/2 и электрическим полем конденсатора W_э= Сu²/2. Эти колебания энергии получили название свободных или собственных. Угловая частота этих колебаний  w_о зависит от параметров отдельных элементов цепи и схемы их соединения. Резонансом называется такой режим электрической цепи, при котором частота свободных колебаний  w_о равна частоте вынужденных колебаний  w, т. е. частоте источника энергии. В резонансном режиме   амплитуды колебаний энергии, а также  соответствующие им амплитуды токов и напряжений, могут достигать значительных величин и превосходить их значения для источника энергии.

Резонанс в цепи с параллельным соединением источника ЭДС Е и  реактивных элементов Lи C получил название резонанса токов. Такой режим наблюдается в цепи при равенстве реактивных проводимостей катушки и конденсатора:   B_L = B_C . Для схемы рис.  8.1 условие резонанса имеет вид: 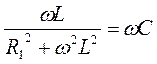 . Это условие может быть достигнуто изменением одного из  параметров элементов схемы: w,L, Cили R₁. Значения параметров отдельных элементов в резонансном режиме определяются в результате решения выше приведенного уравнения:

,   ,    .

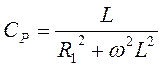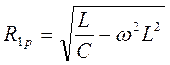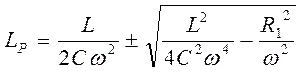В результате решения квадратного уравнения получают два значения индуктивности катушки L_р, что соответствует двум различным точкам резонанса. В тех  случаях, когда решение для параметра оказывается комплексным, резонансный  режим в схеме невозможен.  

Зависимости параметров режима схемы (токов, напряжений) от переменного параметра отдельного элемента называются резонансными характеристиками. В данной работе исследуются резонансные характеристики схемы в функции переменного параметра  С.  Исследования  показывают, что ток источника  в резонансном режиме  имеет  минимальное значение.

Расчет токов в схеме рис. 8.1 целесообразно выполнить в комплексной форме:  ,  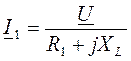,  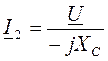 ,  I= I₁ + I₂,     φ = –arg(I).

На рис. 8.2 приведены графические диаграммы  резонансных характеристик в функции переменного параметра  С = var= Cv, построенные в MathCAD.

Рис. 8.2. Графические диаграммы резонансных характеристик.

8.4. Расчетная часть

1. Определить емкость конденсатора С_р из условия резонансного режима в схеме.  Для каждого из заданных отношений С/С_р определить емкость конденсатора С, эквивалентный фазный угол j на входе схемы, комплексные токи в отдельных ветвях I, I₁ и I₂. Результаты расчетов внести в табл.8.2.

2. По результатам расчетов п.1 в выбранных масштабах построить совмещенную графическую диаграмму следующих функций: I, I₁, I₂, j = f(С).

3. Для резонансной точки С = С_р  в выбранных масштабах построить векторные диаграммы токов и напряжений.

4. Определить сопротивление резистора R_1р из условия резонансного