Исследование пассивного четырехполюсника (Лабораторная работа № 18Н)

Министерство образования Республики Беларусь

 

Кафедра “Электротехника и электроника”

Лабораторная работа по ТОЭ №18Н

ИССЛЕДОВАНИЕ  ПАССИВНОГО  ЧЕТЫРЕХПОЛЮСНИКА

М и н с к    2 0 10

Л а б о р а т о р н а я   р а б о т а   №18Н

ИССЛЕДОВАНИЕ  ПАССИВНОГО  ЧЕТЫРЕХПОЛЮСНИКА

18.1. Цель работы

1. Определение коэффициентов пассивного четырехполюсника через параметры элементов Т- или П-схем замещения.

2. Экспериментальное определение входных сопротивлений пассивного четырехполюсника в режимах холостого хода и короткого замыкания.

3. Определение коэффициентов пассивного четырехполюсника через его входные сопротивления в режимах холостого хода и короткого замыкания.

4. Исследование режимов работы пассивного четырехполюсника при различных нагрузках.

18.2.  Исходные данные

Заданы:

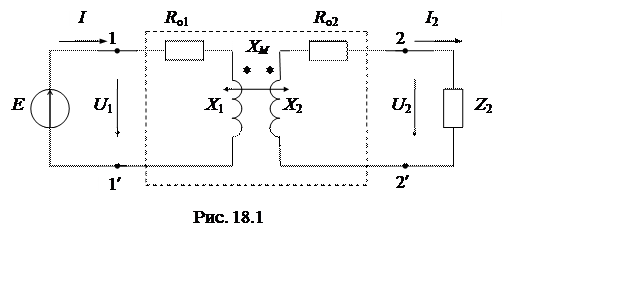
1. Эквивалентная схема исследуемого пассивного четырехполюсника. На входе четырехполюсника действует синусоидальное напряжение U₁, к выходным зажимам подключена нагрузка Z₂ = R₂ – jX_C (рис.18.1).

2. Параметры отдельных элементов схемы (табл.18.1).

3. Рабочие схемы исследуемых цепей и схемы включения измерительных приборов (рис. 18.5 и рис. 18.6).

Т а б л и ц а   18.1

Вариант	1	2	3	4	5	6	7	8	9	10
U1, В	40	45	50	55	60	40	45	50	55	60
w1	0-1	0-2	0-3	0-1	0-2	0-3	0-1	0-2	0-3	0-2
Ro1, Ом	3	4	5	3	4	5	3	4	5	4
Х1, Ом	30	40	50	30	40	50	30	40	50	40
w2	0-2	0-3	0-1	0-3	0-1	0-2	0-2	0-1	0-1	0-3
Ro2, Ом	4	5	3	5	3	4	4	3	3	5
X2, Ом	40	50	30	50	30	40	40	30	40	50
XM, Ом	17	22	19	19	17	22	17	17	19	22
R2, Ом	20	35	30	25	20	25	35	30	40	30
XC, Ом	45	50	55	40	35	40	50	45	55	35

 

3. Теоретические сведения и методические указания

Четырехполюсником называется отдельное устройство или часть сложной электрической цепи (или схемы), содержащая четыре вывода (полюса), два из которых (1 и  1¢)  называются первичными, а два другие (2 и  2¢)  - вторичными. Первичные выводы четырехполюсника подключаются к источнику напряжения (ЭДС), а ко вторичным выводам подключается нагрузка Z₂ = R₂ + jX₂. Уравнения четырехполюсника устанавливают связь между параметрами режима на входе четырехполюсника (U₁, I₁)  с параметрами режима на его выходе (U₂, I₂):

U₁=A·U₂+B·I₂,   I₁=C·U₂+D·I₂,

где А, В, С, D- комплексные коэффициенты четырехполюсника. При определении режимных параметров процессы внутри четырехполюсника не рассматриваются. Между коэффициентами четырехполюсника существует взаимосвязь:                                     A·D-B·C =1.

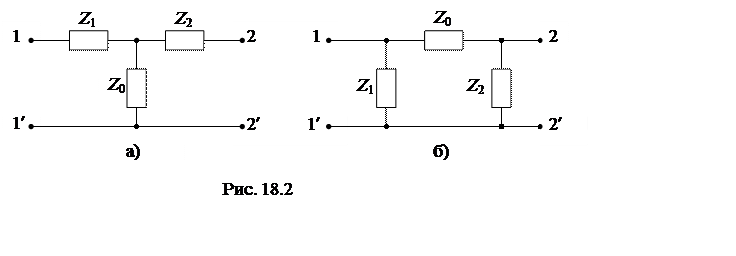
Любой четырехполюсник может быть представлен двумя простейшими эквивалентными схемами, состоящими только из трех элементов: Т-схемой (звездой) и П-схемой (треугольником) (рис.18.2).

Коэффициенты четырехполюсника  могут быть определены через  параметры элементов схем по следующим  уравнениям:

A = 1+Z₁/Z₀,B=Z₁ +Z₂ +Z₁×Z₂/Z₀ , C= 1/Z₀ ,  D= 1+ Z₂/Z₀ - для Т-схемы;

A= 1+ Z₀/Z₂, B= Z₀ , C= 1/Z₁ + 1/Z₂ + Z₀/(Z₁×Z₂) ,  D= 1+Z₀/Z₁ - для  П-схемы.

 

Коэффициенты четырехполюсника  могут быть определены также через его входные сопротивления в режимах холостого хода и короткого замыкания (Z_1X, Z_1K, Z_2X, Z_2K). Входные сопротивления могут быть определены расчетным путем методом свертки  соответствующей схемы четырехполюсника. Эти же сопротивления могут быть определены экспериментально путем выполнения измерений по схеме трех приборов (амперметр + вольтметр + фазометр) (рис. 17.4): Z = (U/I)·e^jj =R + jX, где U, I, j - показания вольтметра, амперметра и фазометра соответственно. Входные сопротивления четырехполюсника связаны с его коэффициентами уравнениями:

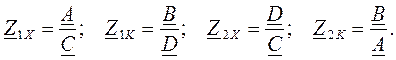
Для определения коэффициентов четырехполюсника через входные сопротивления необходимо решить систему уравнений, составленную из любых 3-х заданных уравнений и уравнения связи между коэффициентамиA·D-B·C= 1. Ниже приведен пример решения такой системы уравнений в маткаде.

Режимные параметры четырехполюсника (токи и напряжения на входе и выходе) определяются путем совместного решения системы уравнений  формы А с уравнением закона Ома для нагрузки. Ниже приведен пример решения такой системы уравнений в маткаде.