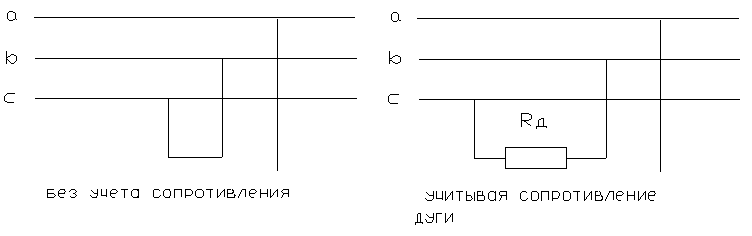
Такое замыкание можно представить, как глухое двухфазное КЗ на ответвлении, фазы которого имеют одинаковое сопротивление Rд/2. Таким приемом несимметричный участок трехфазной цепи приводится к симметричному.
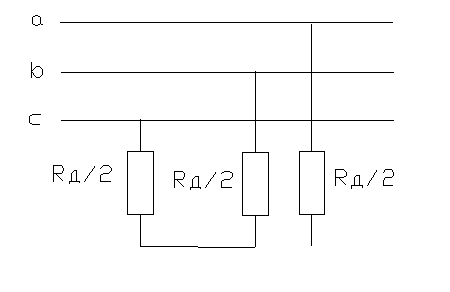
С учетом того, что
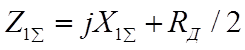
ток прямой последовательности в месте замыкания:
.
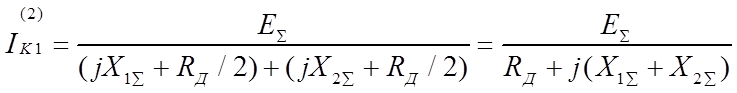Напряжение прямой последовательности:
.
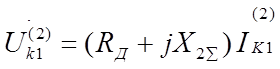Однофазное КЗ. Допустим, что фаза А замкнулась на землю через сопротивление дуги Rд
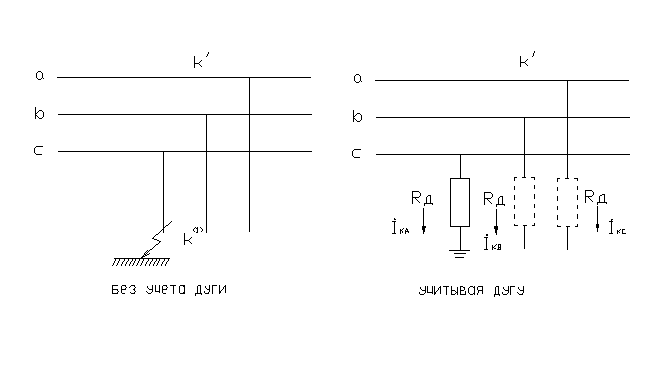
Чтобы сохранить симметрию данного участка трехфазной цепи, можно представить, что такие же сопротивления введены и в две другие фазы. В новых условиях результирующее сопротивление каждой последовательности увеличится на величину Rд, т.е.:
;
;
.
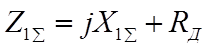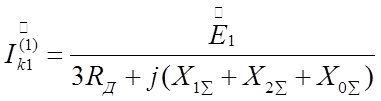Тогда выражение для тока прямой
последовательности в месте КЗ будет:
Напряжение прямой последовательности за
сопротивлением составляет:
.
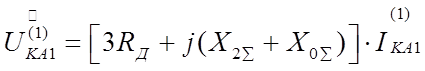2. Двухфазное КЗ на землю.
Для этого вида повреждения сопротивление Rд, очевидно, войдет только в схему нулевой последовательности, причем войдет своей утроенной величиной,
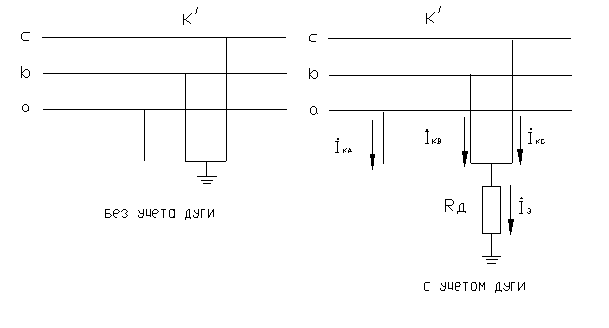
т.е.
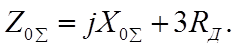
Поэтому выражение для тока прямой последовательности в месте замыкания будет:
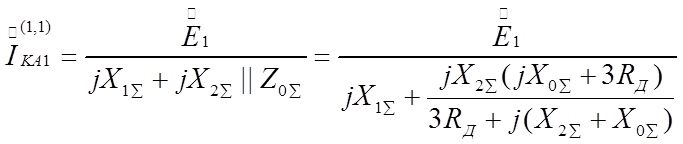
Соответственно напряжение прямой последовательности за сопротивлением Rд.
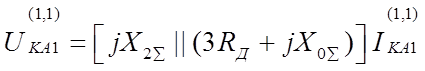
Для определения токов обратной и нулевой последовательностей в месте замыкания служат соответственно выражения из § “Двухфазное КЗ на землю”, в которых вместо
следует ввести 
Поскольку фазы В и С замкнуты между собой накоротко, то независимо от величины Rд соотношение
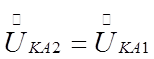
сохраняется, т.е. Uka2 с сопротивлением Rд следует определять по выражению для Uка1. Что касается напряжения нулевой последовательности в точке К´, то
оно, очевидно, равно падению напряжения от тока
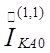в 
.
А4.29 Порядок расчета несимметричных КЗ по расчетным кривым
Расчетные кривые могут быть использованы для определения тока прямой последовательности в любой момент п. п. при любом несимметричном КЗ. Для этого в схеме замещения прямой последовательности в соответствии с правилом Щедрина действительную точку КЗ удаляют на величину шунта, и в новой точке рассматривают симметричное 3-х фазное КЗ.
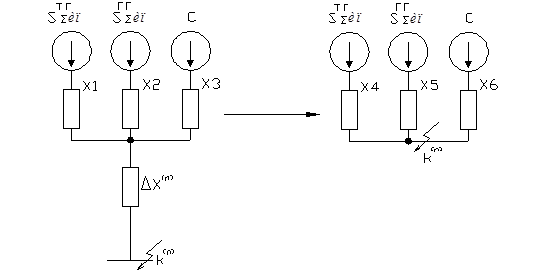
Далее аналогично как для 3-х фазного КЗ определяют расчетные значения сопротивлений всех лучей схемы, кроме луча системы.
,
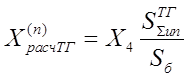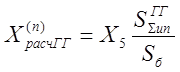
По значению расчетного сопротивления, взяв соответствующие кривые, определяют относительное значение периодической составляющей тока прямой последовательности для интересующих нас моментов времени при рассматриваемом виде КЗ.
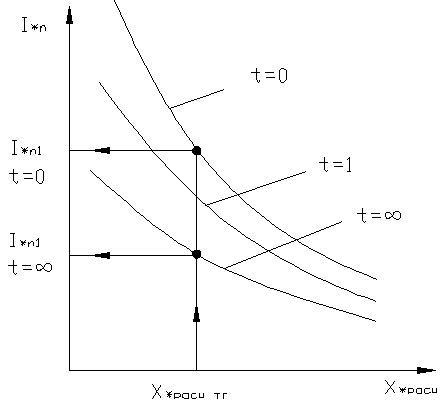Ток прямой последовательности от луча системы будет определяться: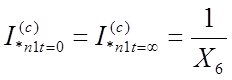 
Для получения действительных значений токов прямой последовательности от каждого луча необходимо умножить относительные значения токов на суммарный номинальный ток соответствующих лучей, а для луча системы – на базисный ток.
; 
;
;
;
.
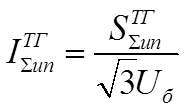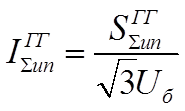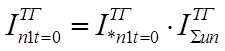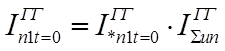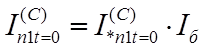Зная суммарный ток прямой последовательности и используя коэффициент пропорциональности m(n), можно определить полный ток в поврежденных фазах для любого несимметричного КЗ
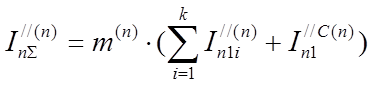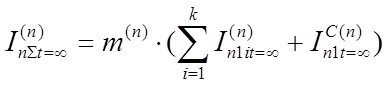, кА;
, кА.
А4. 30 Распределение и трансформация токов и напряжений при несимметричных КЗ
Разные токи и напр. при несимметричных КЗ удобнее всего определять путем суммирования симметричных составляющих этих токов и напр. При этом для определения составляющих токов и напряжений в любой точке и в любой ветви схемы при несимметричном КЗ в к-л конкретной точке находят распределение токов и напр. каждой последовательности в одноименных схемах, пользуясь при этом известными правилами и законами распределения токов и напр в линейных электрических цепях. При определении фазных величин за трансформаторами необходимо иметь в виду, что токи и напр при переходе через трансформатор изменяются не только по величине, но и по фазе в зависимости от группы соединения обмоток Т. Для составления прямой последовательности при трансформации со стороны Y на ∆ происходит поворот вектора на угол е-j30N, а вектор обратной последовательности на угол еj30N , где N- номер группы соединения обмоток Т.
Fa1=FA1* е-j30N*1/k
Fa2=FA2* еj30N*1/k
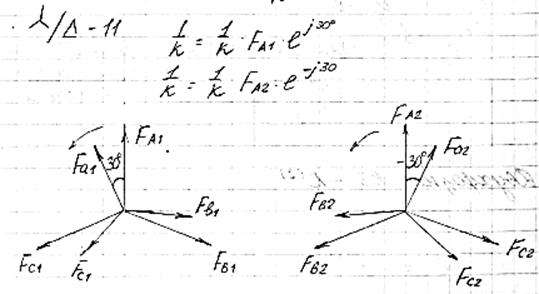
Yo/∆:
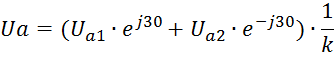
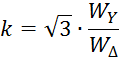
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.