Метод преобразования многолучевой звезды в полный многоугольник (Лабораторная работа № 4), страница 3

U₁-y_1,2¢U₂      -y_1,3¢U₃=J₁¢                      или                  U₁-0,2U₂-0,4U₃=2

y_2,2¢U₂-         y_2,3¢U₃=J₂¢                                                     3U₂-2,4U₃=2

-y_3,2¢U₂+y_3,3¢U₃=J₃¢.                                -2,4U₂+4,2U₃=19.   (7)

Собственно систему уравнений в (7) образуют второе и третье уравнения для неизвестных U₂ i U₃.. Первое уравнение оставлено в системе для формирования системы уравнений с трыянгуляванай матрицей коэффициентов.

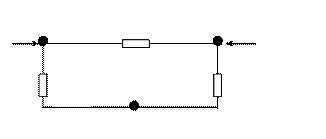А теперь выключим из схемы замещения узел 1. Схема примет вид, приведенный на рис.2. Пользуясь правилами преобразования многолучевой звезды в полный многоугольник, рассчитать параметры этой схемы:                                                                 y_2,3¢=y_2,3+y_1,3y_1,2/y_1,1=2+2´1/5=2,4;¢

y_2,0¢=y_2,0+y_1,2y_1,0/y_1,1=0,2+1´2/5=0,6;

y_3,0¢=y_3,0+y_1,3y_1,0/y_1,1=1+2´2/5=1,8;

J₂¢=J₂+J₁y_1,2/y_1,1=0+10´1/5=2;

Рис. 2.                                                 J₃¢=J₃+J₁y_1,3/y_1,1=15+10´2/5=19.

Сравнивая полученные параметры схемы на рис.2 с другим и третьим уравнением системы (7), приходим к выводу, что система (7) соответствует схеме на рис.2. На этом действия по исключению узлового напряжения U₁ из системы (6) и узла 1 из схемы (2) закончены

Выключим сейчас узловое напряжение U₂ с другого и третьего уравнений системы (7) и, соответственно, выключим узел 2 из схемы на рис.2. Делим второе уравнение на коэффициент y_2,2¢  при U₂, затем умножаем его на коэффициент y_2,2¢ иi отнимаем от третьего уравнения:

U₁  - y_1,2¢ U₂  - y_1,3¢ U₃ = J₁¢      или      U₁ - 0,2 U₂ - 0,4 U₃ = 2  

U₂  - y_2,3¢¢ U₃ =J₂¢¢                              U₂ - 0,8 U₃ = 0,6666

y_3,3¢¢ U₃ =J₃¢¢                                               2,28 U₃ =20,6.            (8)

Собственно систему уравнений в (8) образовывает третье уравнение для неизвестного напряжения U₃.  Второе  уравнение входит в состав системы с трыянгуляванай матрицей коэффициентов.

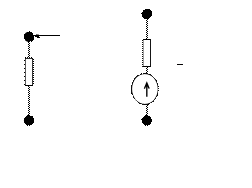
Теперь выключим узел 2 со схемы на рис.2. Узел 2 схемы соответствует второму уравнению системы (7). Схема примет вид, приведенный на рис.3. Пользуясь правилами преобразования многолучевой звезды в полный многоугольник, рассчитаем параметры этой схемы:

 

y_3,0²=y_3,0¢+y_2,3¢y_2,0¢/y_2,2¢=1,8+2,4´0,6/3=2,28;

J₃²=J₃¢+J₂¢ y_2,3¢/y_2,2¢=19+2´2,4/3=20,6;

Z_3,0²=1/y_3,0²=1/ 2,28=0,4386;

E30²

а)                     б)                                 Е_3,0²=J_3,0²/y_3,0²=20,6/2,28=9,035.

Рис.3.

Cхема на рис.3 соответствует третьему уравнению системы (8). Разделив третье уравнение системы (8) на у_3,0²=2,28, приведем матрицу коэффициентов к трыангуляваному виду

:U₁ - y_1,2¢ U₂ - y_1,3¢ U₃ = J₁¢    или      U₁ - 0,2 U₂ - 0,4 U₃ = 2

U₂ - y_2,3² U₃ = J₂²                                U₂ - 0,8 U₃ = 0,6666

U₃ = J₃²¢                                                     U₃ = 9,035.     (9)

На этом прямой ход метода Гаусса для системы узловых уравнений (6) закончен. Для схемы замещения на рис.1 это эквивалентно "свёртке" схемы к узлу 3 (рис.3). Проводимость y_3,0² и ток J₃  называют соответственно эквивалентными, или результативными, проводимостью и током источника тока схемы относительно узла 3. Если перейти от параметров источника тока к параметрам источника ЭДС (рис.3б), то получим эквивалентное, или результативное, сопротивление схемы Z_3,0² и эквивалентную, или результативную, ЭДС схемы Е_3,0² относительно третьего узла. При этом эквивалентная ЭДС Е_3,0²    численно  равна узловому напряжению U₃ для нормального режима, а ток эквивалентного источника тока J_3,0² - полному току короткого замыкания в узле 3.

Выполним обратный ход метода Гаусса для трыангуляванай системы (9) и рассчитаем узловые напряжения:

.U₃=9,035 В;

U₂=J₂¢¢+y_2,3¢¢U₃=0,6666+0,8´9,035=7,895 В;

U₁=J₁¢+y_1,2¢U₂+y_1,3¢U₃=2+0,2´7,895+0,4´9,035=7,193 В.

По известным узловым напряжениям для нормального режима рассчитать токи в отраслях схемы на рис.1 (положительное направление - от узла с большим номером к узлу с меньшим номером):