Новые эначения элементов, например, последней n-ой строки матриц
Y¢ и J¢ будут иметь значения:
:yn,1¢=yn,1+ yi,1 yn,j/yi,j; yn,2¢=yn,2+yi,2 yn,j/yi,j; ... yn,j-1¢=yn,j-1+ yi,j-1 yn,j/yi,j; ...
yn,j+1¢=yn,j+1+ yi,j+1 yn,j/yi,j; yn,n¢=yn,n+ yi,n yn,j/yi,j; Jn¢=Jn + Ji yn,j/yi,j . (3)
В формулах (3) индекс i (номер уравнения системы (1)) равен индексу j (номеру узла схемы). В формуле (3) при i = j находятся суммы проводимость ветвей, подключенных к j-тому узлу (собственная проводимость узла). Анализируя формулы (3), можно сформулировать правила, которые позволяют рассчитать параметры ветвей схемы после выключения j-того узла схемы: а) проводимость ветви схемы yn,k, которая включена между n-ым i k-ым узлами, на которые опиралась многолучевая звезда с выделенным узлом j, получает прирост, который равен произведению проводимостей yn,j i yj,k тех двух лучей звезды, которые связывали выдаляемый узел j с вершинами n i k многоугольника, деленному на сумму проводимостей ветвей многолучевой звезды yj,j (собственная проводимость выделяемого узла):
yn,k¢=yn,k + yn,j yj,k / yj,j. (4)
Если между узлами n i k ветвь отсутствовала, то после выключения узла j между этими узлами возникает новая ветвь схемы с проводимостью, равной приросту проводимости. Количество всех новых ветвей и приростов определяется формулой сочетаний;
б) ток источника тока Jn в n-ом узле многоугольника получает прирост, который равен произведению тока источника тока Jj в выдаляемым j-том узле на проводимость луча yn,j звезды, деленному на сумму проводимость ветвей многолучевой звезды yj,j:
Jn¢=Jn + Ji yn,j / yi,j . (5)
Если в n-ом узле многоугольника перед удалением j-того узла источник тока отсутствовал, то после удаления узла j там возникает новый источник тока с током, равным приросту. Количество новых источников тока или приростов источников тока равно количеству вершин многоугольника.
Применяя
далее алгоритм исключения других неизвестных узловых напряжений в системе (1) и записывая
исключенные уравненния
в виде системы, можно привести эту систему к виду, когда матрица коэффициентов Y
превратится в верхнюю треугольную матрицу. а)
 |
|||
|
|||
б)
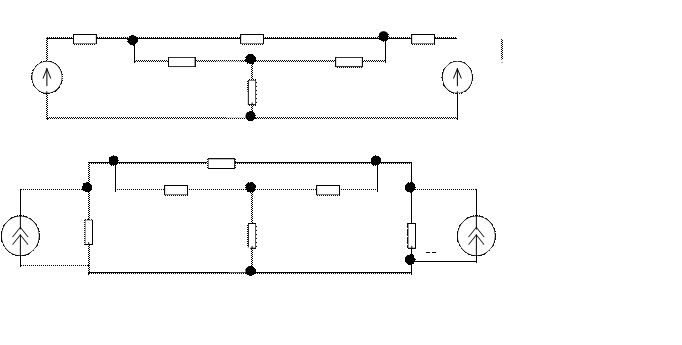
Z10=0,5; Z20=5; Z30=1; y10=2; y20=0,2; y30=1;
Z12=1; Z13=0,5; Z23=0,5; y12=1; y13=2; y23=2;
E1=5; E3=15; J1=10; J3=15.
Рис.1. Схема замещения энергосистемы: а) ветви представлены сопротивлениями (Ом) и ЭДС (В); б) ветви представлены проводимостями (См) и токами источников тока (А).
На этом заканчивается прямой ход метода Гаусса. Для схемы прямой ход соответствует “свёртке” этой схемы к одному из ее линейно независимых узлов. При этом каждая строка матрицы Y содержит информацию об удаляемых многолучевых звездах на момент их удаления.
При выполнении обратного хода метода Гаусса в системе с трыангуляванай матрицей выполняется расчет неизвестных узловых напряжений U. Для схемы этот этап соответствует “развертыванию”; ее и восстановлению удаленных узлов. На каждом этапе обратного хода используется информация соответствующего строки трыангуляванай матрицы Y и матрицы J.
Пример: Рассчитать токи нормального режима в ветвях схемы на рис. 1а методом преобразования многолучевой звезды в полный многоугольник. Система узловых уравнений в общей форме и с численными коэффициентами:
y1,1U1 - y1,2U2 - y1,3U3 = J1 5U1 - 2 U2 - 2 U3 = 10
- y2,1U1 + y2,2U2 - y2,3U3 = J2 -2 U1 + 3,2 U2 - 2 U3 = 0
-y3,1U1 - y3,2U2 + y3,3U3 = J3, - 2U1- 2 U2 + 5 U3 = 15. (6)
Поделим уравнение системы (1) на y1,1=5, затем умножим его сначала на- y2,1=-1 i отнимет его от второго уравнения системы, затем умножим его на-y3,1=-2 и отнимет от третьего уравнения, в результате чего получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.