Министерство образования Республики Беларусь
Белорусский Национальный Технический Университет
Военно-технический факультет
Курсовая работа по “Информатике”
Программное обеспечение для построения полей изолиний
Подготовил: курсант группы 115214
Амельянчик А.И.
Руководитель: Новиков А.А.
Минск 2006
1. Разработанное программное обеспечение служит для автоматизации задачи построения изолинии, для функций заданных дискретным набором точек. В программе реализован алгоритм вычисления точек пересечения пространственных треугольников и плоскости изолинии (поверхности уровня) , с последующим построением линии по вычисленным координатам. Так же в программе реализовано построение триангуляционной сетки , на которую была разбита заданная область определения фрагмента поверхности , и введен элемент управления курсор. Курсором можно указать точку в которой выводится отметка уровня поверхности (репер).
2. Постановка задачи.
Для проведения линии уровня нам сначала следует разбить заданную область определения поверхности на треугольники, то есть провести её триангуляцию {xi,yi} и значения zi для каждой пары {xi,yi}.
2.1 Физический и геометрический смысл.
Многие свойства месторождений полезных ископаемых мощность пласта, глубина залежей и т.д. формально могут быть описаны как функции двух переменных, которые в пространстве представляют собой некоторые поверхности (реальные или условные). Одним из основных методов отображения таких поверхностей в горной геометрии является способ изолиний. Также изолинии применяются для построения рельефа местности как основной приём картостроения.
Геометрический смысл линии уровня заключается в том, что изолиния – это поверхность, полученная при пересечении плоскости, и поверхности заданного.
2.2 математические постановка задачи.
Для решения вопроса положения изолиний на плоскости необходимо вычислить положение изолиний в каждом треугольнике, моделирующем поверхность. То есть надо найти линию пересечения пространственного треугольника с плоскостью, определяющей значение изолинии. Проекция этого отрезка на плоскость xOy и является отдельным отрезком изолинии.
Обозначим 
, 
, 
координаты трёх вершин, образующих
пространственный треугольник (фрагмент поверхности). Уравнение горизонтальной
плоскости изолинии
. Ребро треугольника ab пересекает плоскость изолинии , если 
и 
, либо 
и 
в противном случае ребро треугольника ab лежит вне плоскости .
Для нахождения координат линий пересечения треугольника с плоскостью достаточно найти координаты пересечения плоскости и каждой стороны треугольника. Для этого следует рассмотреть каждое из ребер треугольника.
Сначала определяем: пересекает вообще пространственный треугольник плоскость изолинии или нет, или он полностью лежит в этой плоскости. Для этого служат следующие неравенства:
, тогда
сторона треугольника принадлежит плоскости, если 
(
) и 
(
), то
сторона треугольника не лежит в данной плоскости(Z0). Если ни одно из этих условий не выполняется, то
точка пересечения грани треугольника и плоскости находится следующим образом:
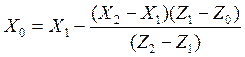
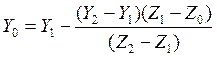, где
X1, Y1, Z1-
координаты первой вершины ребра, X2, Y2, Z2-
координаты второй вершины ребра, Z0-
координата Z пересечения плоскости и грани треугольника.
Решая эти уравнения для каждого ребра треугольника, получаем линию пересечения плоскости и треугольника. Последовательно перебирая все треугольники, получаем всю изолинию данного уровня.
2.3 Исходящие данные.
Ввод первоначальных данных осуществляется: с клавиатуры - положение верхнего правого угла окна, в котором размещается изображение и длинна окна (X0, Y0, Lx, Ly),а также уровень требуемой изолинии(z0), с помощью текстового файла задаются координаты точек и последовательность их соединения в треугольники. Текстовый файл имеет следующую структуру: в первой строке задаётся количество точек для построения сетки, далее задаются координаты(x, y, z) всех точек, причём в каждой строке находится описание только одной точки, затем задаётся количество треугольников, в которые объединяются данные точки и последовательность их соединения в треугольник. В каждой строке указываются номера трёх точек, образующих треугольник. Эти параметры находятся в программе в следующих переменных: Nt -количество точек, XYZ -массив для хранения координат точек, Ntr -количество треугольников, NNN- массив для хранения точек, образующих треугольники. Структура массивов XYZ и NNN следующая. XYZ - двумерный массив, в который передаётся номер точки и три её координаты, NNN -двумерный массив, в который передаётся номер треугольника и номера точек, образующего его.
Файл данных имеет следующий вид:
8
2 2 11
1 4 7
2 5 7
3 4 32
5 3 158
5 5 168
7 4 1074
5 1 148
8
1 2 4
2 3 4
3 4 6
4 6 5
6 5 7
7 5 8
8 5 4
8 4 1
3. Управление программой. Управление осуществляется при помощи курсора, который управляется с клавиатуры: клавиши влево, вправо, вниз, вверх предназначены для перемещения курсора по экрану; клавиша Enter служит для вывода в текущем месте экрана репера, клавиша Tab убирает, рисует треугольную сетку; клавиша Esc служит для выхода из программы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.