БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Энергетический факультет
Кафедра “ Электрические станции ”
РАЗРАБОТКА АЛГОРИТМА И ПРОГРАММЫ РАСЧЕТА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
КУРСОВАЯ РАБОТА
По дисциплине “ Информатика ”
Руководитель: доцент Булат В. А.
Исполнитель : студент гр. 106117
Минюк А. Г.
Минск-2008г.
Введение
Интенсивное развитие технологических процессов тесно связано с применением электронной техники, преимущественно цифровых вычислительных машин. Поэтому при обучении инженеров-электриков особое внимание должно уделяться их компьютерной подготовке. Инженер должен уметь ²общаться² с ЭВМ, работать на ней, знать основы программирования на алгоритмических языках при решении разнообразных технических, экономических и научных задач, уметь использовать ЭВМ в своей будущей профессиональной деятельности.
В учебном процессе знания вычислительной техники и программирования также необходимы, поскольку ряд специальных дисциплин, учебных, курсовых и дипломных проектов, учебно-исследовательских работ выполняются с применением ЭВМ или полностью на них.
Цель курсовой работы: закрепление студентами практических навыков программирования на алгоритмическом языке высокого уровня FORTRAN на примере составления и отладки программы для решения электротехнической задачи, ознакомление со специальной терминологией, приобретение навыков написания и оформления программ. Это дает дополнительные возможности студентам успешно применять средства вычислительной техники в процессе обучения в университете и в дальнейшем на практике.
1. Постановка задачи
Задание предусматривает расчет электрической цепи, к которой приложено синусуидальное напряжение, с использованием библиотеки стандартных подпрограмм (программа вывода расчета в виде графиков), а также разработки подпрограммы вычисления опрделенного интеграла методом прямоугольников для расчета действующих значений токов в ветвях и напряжений на реактивных элементах.
В соответствии с исходными данными расчётная схема имеет следующий вид (рис.1.1):
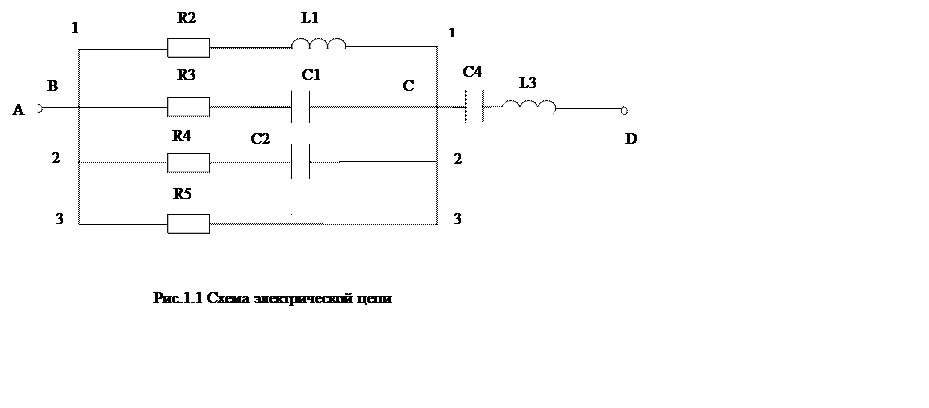
|
N |
R2 |
R3 |
R4 |
R5 |
С1 |
C2 |
C4 |
L1 |
L3 |
Um |
Q |
Q1 |
Q2 |
F |
|
Ом |
Ом |
Ом |
Ом |
мкФ |
мкФ |
мкФ |
мГн |
мГн |
В |
В |
В |
Гц |
||
|
11 |
15 |
500 |
85 |
500 |
8000 |
400 |
530 |
7 |
17 |
640 |
U |
640 |
990 |
111 |
Для нахождения тока в цепи и ее ветвях, рассчитывается полное сопротивление электрической цепи, используя комплексное представление сопротивления.
Определим параметры элементов электрической схемы:
Индуктивное сопротивление катушки индуктивности L1:
![]() ;
;
Индуктивное сопротивление катушки индуктивности L3:
![]()
![]()
![]()
Емкостное сопротивление конденсатора С2:
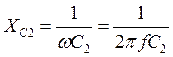 ;
;
Емкостное сопротивление конденсатора С1:
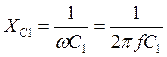 ;
;
Емкостное сопротивление конденсатора С4:
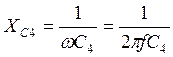
Рассчитываем сопротивление отдельных участков схемы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассчитаем общее сопротивление параллельных ветвей схемы:
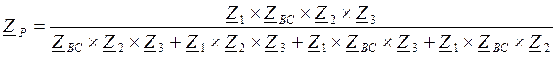
Рассчитаем общее сопротивление схемы:
![]()
Пусть есть комплексное число ![]() , тогда
, тогда ![]() .
.
Амплитудные значения токов и напряжений всей схемы и отдельных ее частей:
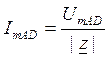
Так как через последовательно соединенные элементы протекает один и тот же ток, то напряжение на параллельно соединенных ветвях будет рассчитываться по формуле:
![]()
Тогда амплитудные значения токов на параллельно соединенных ветвях будут соответственно находиться по формулам:
Ток в первой ветви:
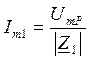
Ток в ветви ВС:
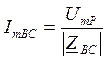
Ток во второй ветви:
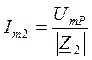
Ток в третьей ветви
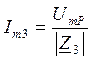
Амплитудное значение напряжения на катушке L3 рассчитывается по формуле:
![]()
Амплитудное значение напряжения на конденсаторе С2 рассчитывается по формуле:
![]()
Находим углы сдвига в неразветвленной части цепи и ее ветвях, используя амплитуды токов. Для нахождения углов определяется вещественная (Re) и мнимая (Im) часть комплексного числа. В зависимости от этих величин определяется угол:
Угол сдвига фаз между током и напряжением в ветви АД равен:
![]()
Угол сдвига фаз между током и напряжением в первой ветви равен:
![]()
Угол сдвига фаз между током и напряжением в ветви ВС равен:
![]()
Угол сдвига фаз между током и напряжением во второй ветви равен:
![]()
Угол сдвига фаз между током и напряжением в третьей ветви равен:
![]()
Угол сдвига фаз между током и напряжением в ветви CD равен:
![]()
Таким образом, закон изменения тока в электрической цепи и ее ветвях имеет вид:
![]() ;
;
Закон изменения напряжения на зажимах АД:
![]()
Законы изменения напряжения на индуктивности L3 и емкости С2 соответственно будут:
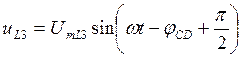
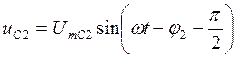
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.