Классическое и статистическое определение вероятности. Наивероятнейшее число появлений события в независимых испытаниях. Формула полной вероятности

отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В (х) и С(у). Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей к ней точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Решение. Представим, что ОВ(х)=х, ОС(у)=у. Тогда отрезок В(х)С(у)=ОС(у)-ОВ(х)=у-х. Если отрезок ВС по длине меньше ОВ, то это можно записать как у-х<x

y<2x_

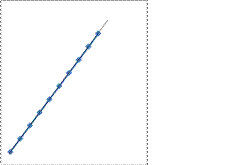
Данным неравенством может быть выражена определённая область на графике в координатах у_L(x_L).

.

Как можно заметить из графика, искомая вероятность составляет ¾.

VII.

Наивероятнейшее число появлений события в независимых испытаниях

Чему равна вероятность р=0.3 наступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?

Решение. Вероятность наступления события в течение каждого из 49 испытаний постоянна и равна р=0.3. Следовательно, вероятность ненаступления события в каждом испытании также постоянна и равна q=1-p=1-0.3=0.6.

Искомая вероятность по формуле Бернулли равна

VIII

ОСНОВНЫЕ ТЕОРЕМЫ

Брошены три игральные кости. Найти вероятности следующих событий:

а) на двух выпавших гранях появится одно очко, а на третьей грани - другое число очков;

б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани—другое число очков;

в) на всех выпавших гранях появится разное число очков.

Решение.

а) Вероятность выпадения 1 очка у первой и второй костей

Р(A)=P(B)=1/6

Вероятность выпадения другого количества очков у третьей кости, вычисленная с учётом невозможности выпадения 1 очка:

Р(С)=5/6

Искомая вероятность, вычисленная по формуле произведения вероятностей:

P(ABC)=(1/6)*(1/6)*(5/6)=5/216

б)

в)Вероятность выпадения любого количества очков у первой кости:

Р(А)=1/6

Вероятость невыпадения количества очков первой кости у второй кости:

Р(В)=5/6

Вероятность того, что результат третьей кости не совпадает с результатами первой и второй:

Р(С)=4/6=2/3

Искомая вероятность, вычисленная по формуле произведения вероятностей:

Р(АВС)=(1/6)*(5/6)*(2/3)=5/54

IX

Формула полной вероятности

В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30%—с заболеванием L, 20%—с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К?

P(B1)	P(B1)	вероятность полного излечения
K, В1	50%	0,5	0,7
L, В2	30%	0,3	0,8
M, В3	20%	0,2	0,9

Решение. Обозначим через А событие, состоящее в том, что больной был выписан здоровым. Можно сделать 3 предположения:

1)  больной болел заболеванием К (гипотеза В₁)

2)  больной болел заболеванием L (гипотеза В₂)

3)  больной болел заболеванием M (гипотеза В₃)

Искомую вероятность того, что больной болел заболеванием K, найдём по формуле Бейеса:

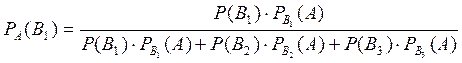
По условию задачи имеем:

P(B₁)=0,5 (вероятность того, что больной болел заболеванием К);

P(B₂)=0,3 (вероятность того, что больной болел заболеванием L);

P(B₃)=0,2 (вероятность того, что больной болел заболеванием M);

=0,7 (вероятность полного излечения от болезни K);

=0,8 (вероятность полного излечения от болезни L);

=0,9 (вероятность полного излечения от болезни M);

Искомая вероятность

.

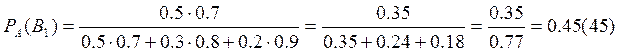X

Схема Бернулли

Отдел технического контроля проверяет партию из 10 деталей. Вероятность того, что деталь стандартна, равна 0,75. Найти наивероятнейшее число деталей, которые будут признаны стандартными.

Решение.

Здесь число n опытов (количество деталей) равно 10, p – вероятность того, что деталь стандартна, равна 0.75, q=1–p=0.25. В рассматриваемом случае np – q

=10*0.75−0.25=7,25–нецелое число, единственное искомое наивероятнейшее число m0 стандартных деталей определяется из условий np–q<m0<np+p, в нашем