Двумерные дискретные/непрерывные случайные величины

РГР2.  Случайные величины.

Двумерные дискретные случайные величины

Задача №1 .

·  Описать закон распределения случайного вектора (X,Y)

·  Описать законы распределения отдельных компонент

·  Найти ковариационную (корреляционную) матрицу

·  Найти условные законы и условные мат. ожидания

·  Найти функцию распределения

·  Установить зависимость компонент X и Y

Двумерные непрерывные случайные величины

Задача №2 .

Найти:

1.  выражение для   

2.  одномерные плотности  

3.  центр рассеивания

4.  сделать вывод о зависимости X и Y

5.  найти

6.  плотности условных распределений

Пусть () – вероятностное пространство (- пространство элементарных событий, S - -алгебра событий, -вероятности событий);  - множество вещественных чисел.

Будем обозначать случайную величину, - принимаемые этой величиной значения.

Определение.  Случайной величиной называется числовая функция, определённая на пространстве элементарных событий , которая каждому элементарному событию ставит в соответствие число  : , причем функция должна быть такова, чтобы событие принадлежало -алгебре событий S, то есть для любого определена вероятность .

Определение. Функцией распределения случайной величины называется функция , которая равна вероятности события :

Тогда есть неубывающая, непрерывная слева функция, удовлетворяющая свойствам:

1. 

2. 

3. 

Дискретные случайные величины

Определение. Случайная величина, принимающая конечное или счётное число значений, называется дискретной.

Определение. Закон распределения дискретной случайной величины представляет собой таблицу, в которой значениям, принимаемым случайной величиной, сопоставлены их вероятности, причём, события  образуют полную группу событий, то есть 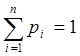(условие нормировки):

Функция распределения дискретной случайной величины.

Основные численные характеристики: начальный момент, центральный момент, математическое ожидание, дисперсия

Определение. Начальный момент порядка k:

В случае дискретной случайной величины:

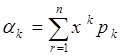
В случае непрерывной случайной величины:

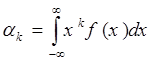
Определение.  Математическое ожидание

Определение. Дисперсия

Определение. Среднее квадратическое отклонение

Свойства

MX	DX

Определение. Центральный момент порядка k:

Для дискретной случайной величины:

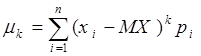
Для непрерывной случайной величины:

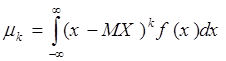
В частности,

Непрерывные случайные величины

Плотность распределения.

Определение. 

Свойства.

1. 

2. 

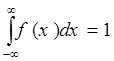
3. 

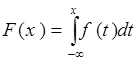
4. 

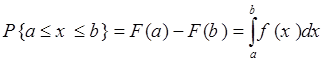
Равномерный закон распределения.

Определение. Равномерное распределение на отрезке:

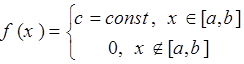
Определение. Равномерное распределение в области D площадью S_D:

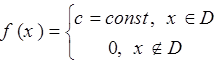
Задачи из теста

График функции распределения имеет вид:

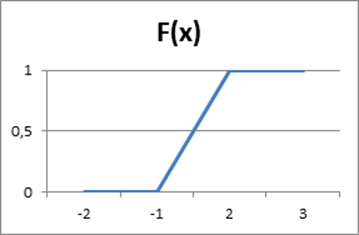
Найти  математическое ожидание MX.

Двумерные случайные величины

Дискретные двумерные случайные величины.

Пусть случайные величины и  имеют законы распределения:

и

Определение 5. Случайные величины и называются независимыми, если независимы события и .

·  Описать закон распределения случайного вектора (X,Y)

Пусть дискретная двумерная случайная величина (X,Y) задана распределением:

Из распределения двумерной случайной величины можно получить законы распределения для одномерных случайных величин:

·  Описать законы распределения отдельных компонент

·  Найти ковариационную (корреляционную) матрицу

Определение. Ковариацией называется

Определение. Коэффициентом корреляции называется

Определение. Ковариационной матрицей называется

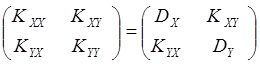
·  Найти условные законы и условные мат. ожидания

·  Найти функцию распределения

·  Установить зависимость компонент X и Y

Непрерывные  двумерные случайные величины.

1.  выражение для  

2.  одномерные плотности  

3.  центр рассеивания

4.  сделать вывод о зависимости X и Y

5.  найти

6.  плотности условных распределений