


Дано:
ОА = 25 см;
АВ = 80 см;
АС = 20 см;
ωОА = 1 рад/с;
εОА = 2 рад/с2.
Найти:
VA, VC, VB, WA, WB, WC, ωAB, εAB - ?
Решение
I. Определение скоростей.
1). VA =ωОА•OA = 1•25 = 25 см/с;
2). Проводим ![]() и
и
![]() и пересечением перпендикуляров к
и пересечением перпендикуляров к ![]() и
и ![]() (из
точек А и В) получаем точку СV – мгновенный центр скоростей звена АВ.
(из
точек А и В) получаем точку СV – мгновенный центр скоростей звена АВ.
Соединяем СV с С и проводим ![]() .
.
Если ωAB – есть угловая скорость поворота звена АВ вокруг полюса СV, то:
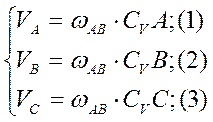
Из прямоугольника треугольника ABCV имеем:
СVA = 2AB = 2•80 = 160 см .
СVB = СVA•cos300 = 160•0,866 = 138,56 см .
Из прямоугольного треугольника СВСV по теореме Пифагора: ![]() , где ВС = АВ – АС = 80 – 20 = 60 см, т.е.:
, где ВС = АВ – АС = 80 – 20 = 60 см, т.е.:
![]() см, тогда из равенства (1):
см, тогда из равенства (1):
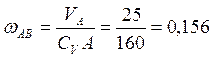 рад/с
рад/с
Из равенства (2):
VB = 0,156•138,56 = 21,65 см/с
Из равенства (3):
VC = 0,156•151 = 23,6 см/с .
По теореме о проекциях скоростей двух точек на проходящую через них прямую имеем:
VB•cos0 = VA•cos300, VС•cosα =
VA•cos300, где 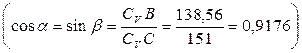 , откуда:
, откуда:
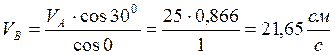 ,
,
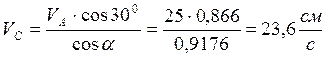 .
.
II. Определение ускорений.
1). Ускорение точки А:
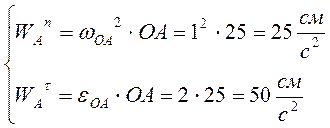 , так
что:
, так
что:
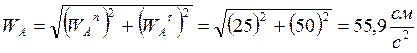
2). Т.к. ускорение точки А известно, то принимаем ее за полюс, тогда:
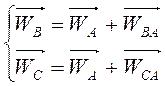 или
или 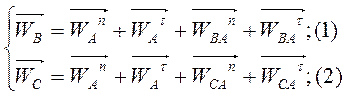 .
.
Запишем уравнение (1) в проекциях на оси x, y:
(3) ![]() ;
;
(4) ![]() .
.
Здесь: 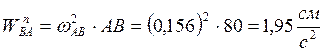 .
.
Из уравнения (3): 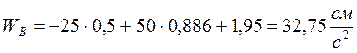 .
.
Из уравнения (4): 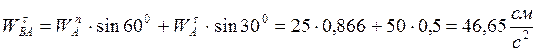 .
.
И т.к. ![]() , то
, то 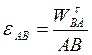 , т.е.:
, т.е.:
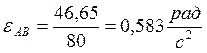 .
.
3). Запишем уравнение (2) в проекциях на оси x, y:
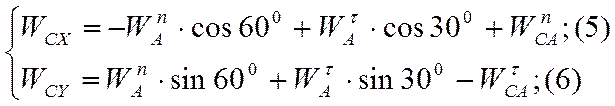 , где
, где
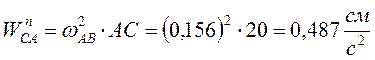 ,
,
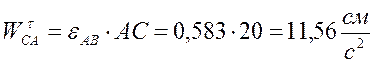 ,
тогда:
,
тогда:
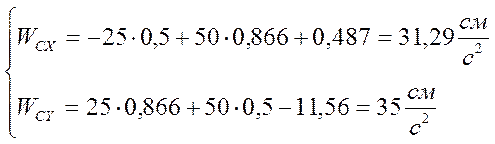 , тогда:
, тогда: 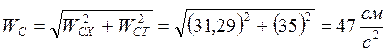 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.