









program KURSACH1
|
a=1 |
|
b=3 |
|
step=0.1 |
|
eps=0.0001 |
|
open(1,file='c:\FLA\SE-71\data') |
|
do x=a,b,step |
|
f = fu(x) |
|
if (a>b) then |
|
write (1) 'incorrect input' |
|
else |
|
print *,'f(x) = ',f |
|
write (1,*) x,f |
|
end if |
|
2 f1 = fu(a) |
|
f2 = fu(b) |
|
if (f1*f2<0) then |
|
c = (a+b)/2 |
|
fc = fu(c) |
|
else |
|
print *,'root was not found' |
|
end if |
|
if (f1*fc<0) then |
|
b = c |
|
else |
|
a = c |
|
endif |
|
if ((b - a)<eps) then |
|
print *,'f',c |
|
else |
|
goto 2 |
|
endif |
|
enddo |
|
end program KURSACH1 |
|
function fu(x) |
|
fu=1./2*exp(-x/2)+3./2*asin(1./3*cos(x)) |
|
end function fu |
|
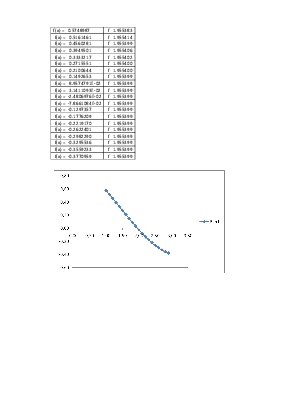
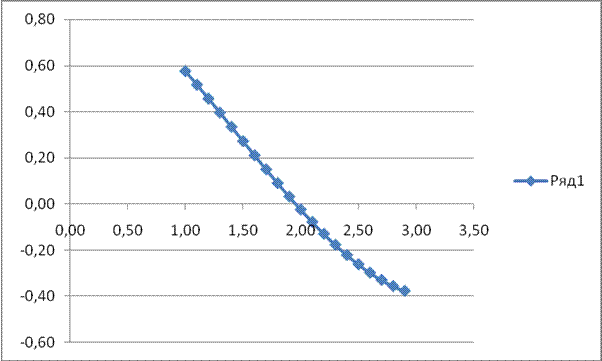
f(x) = 0.5748987 |
f 1.955383 |
|
f(x) = 0.5161461 |
f 1.955414 |
|
f(x) = 0.4560281 |
f 1.955399 |
|
f(x) = 0.3949501 |
f 1.955406 |
|
f(x) = 0.3333217 |
f 1.955402 |
|
f(x) = 0.2715551 |
f 1.955400 |
|
f(x) = 0.2100644 |
f 1.955400 |
|
f(x) = 0.1492653 |
f 1.955399 |
|
f(x) = 8.9574791E-02 |
f 1.955399 |
|
f(x) = 3.1411093E-02 |
f 1.955399 |
|
f(x) = -2.4806976E-02 |
f 1.955399 |
|
f(x) = -7.8661084E-02 |
f 1.955399 |
|
f(x) = -0.1297357 |
f 1.955399 |
|
f(x) = -0.1776209 |
f 1.955399 |
|
f(x) = -0.2219170 |
f 1.955399 |
|
f(x) = -0.2622401 |
f 1.955399 |
|
f(x) = -0.2982290 |
f 1.955399 |
|
f(x) = -0.3295536 |
f 1.955399 |
|
f(x) = -0.3559233 |
f 1.955399 |
|
f(x) = -0.3770959 |
f 1.955399 |
Определить значение определенного
интеграла 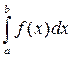 . В качестве подынтегральной функции и интервала
интегрирования использовать данные табл.1.
. В качестве подынтегральной функции и интервала
интегрирования использовать данные табл.1.
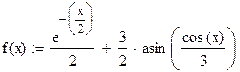
1.
|
|
|
|
|
|
2.
program REZ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.