|
-7.7000000E-02 -0.1100000 -0.2500000 |
ITTERATIONS mpi 1.000000 |
1.4100000E-02 2.0928994E-02 -0.1690400 |
|
ITTERATIONS mpi 2.000000 |
-4.0181540E-02 -2.6565701E-02 -0.2651946 |
ITTERATIONS mpi 3.000000 |
|
-3.7942603E-03 2.5691286E-02 -0.2222451 |
ITTERATIONS mpi 4.000000 |
-2.8118446E-02 1.4147311E-03 -0.2606331 |
|
ITTERATIONS mpi 5.000000 |
-1.2209557E-02 2.2481665E-02 -0.2399799 |
ITTERATIONS mpi 6.000000 |
|
-2.2850256E-02 1.0930091E-02 -0.2559268 |
ITTERATIONS mpi 7.000000 |
-1.5860133E-02 1.9722849E-02 -0.2464540 |
|
ITTERATIONS mpi 8.000000 |
-2.0514429E-02 1.4448255E-02 -0.2532429 |
ITTERATIONS mpi 9.000000 |
|
-1.7445825E-02 1.8201053E-02 -0.2489952 |
ITTERATIONS mpi 10.00000 |
-1.9483473E-02 1.5840933E-02 -0.2519251 |
|
ITTERATIONS mpi 11.00000 |
-1.8137373E-02 1.7462775E-02 -0.2500415 |
ITTERATIONS mpi 12.00000 |
|
-1.9029941E-02 1.6417339E-02 -0.2513153 |
ITTERATIONS mpi 13.00000 |
-1.8439684E-02 1.7122954E-02 -0.2504848 |
|
ITTERATIONS mpi 14.00000 |
-1.8830776E-02 1.6662240E-02 -0.2510407 |
ITTERATIONS mpi 15.00000 |
|
-1.8572006E-02 1.6970322E-02 -0.2506756 |
ITTERATIONS mpi 16.00000 |
-1.8743392E-02 1.6767830E-02 -0.2509187 |
|
ITTERATIONS mpi 17.00000 |
-1.8629964E-02 1.6902581E-02 -0.2507584 |
ITTERATIONS mpi 18.00000 |
|
-1.8705077E-02 1.6813695E-02 -0.2508648 |
ITTERATIONS mpi 19.00000 |
-7.7000000E-02 -0.1040710 -0.1718266 |
|
ITTERATIONS mz 1.000000 |
-6.9848821E-03 -2.3548849E-02 -0.2362778 |
ITTERATIONS mz 2.000000 |
|
-1.1807851E-02 9.0480968E-03 -0.2497656 |
ITTERATIONS mz 3.000000 |
-1.6911101E-02 1.6184971E-02 -0.2511807 |
|
ITTERATIONS mz 4.000000 |
-1.8412914E-02 1.7008156E-02 -0.2509969 |
ITTERATIONS mz 5.000000 |
|
-1.8672891E-02 1.6936272E-02 -0.2508644 |
ITTERATIONS mz 6.000000 |
-1.8687341E-02 1.6871110E-02 -0.2508282 |
|
ITTERATIONS mz 7.000000 |
Варианты задания даны в таблице 3.
|
16 |
y’=x+ctg(x-1/y) |
y(2)=-1, xÎ [2,4] |
program PROGRAM4
|
parameter (n=10) |
|
dimension x(n),y(n) |
|
a=2 |
|
b=4 |
|
h=(b-a)/n |
|
y(1)=1 |
|
x(1)=a |
|
open (1,file='C:\FLA\program4.dat') |
|
write (1,*),x(1),y(1) |
|
do i=2,n |
|
x(i)=x(i-1)+h |
|
end do |
|
do i=2,n |
|
y(i)=y(i-1)+fxy(x(i-1),y(i-1))*h |
|
write (1,*),x(i),y(i) |
|
write (*,*),x(i),y(i) |
|
end do |
|
close (1) |
|
open (2,file='C:\fla\program5.dat') |
|
write (1,*),x(1),y(1) |
|
do i=2,n |
|
x(i)=x(i-1)+h |
|
end do |
|
do i=2,n |
|
xi=x(i-1) |
|
yi=y(i-1) |
|
yi=y(i-1)+0.5*h*fxy(xi,yi) |
|
y(i)=y(i-1)+h*fxy(xi+0.5*h,yi) |
|
write (2,*),x(i),y(i) |
|
write (*,*),x(i),y(i) |
|
end do |
|
close (2) |
|
end program PROGRAM4 |
|
function fxy(x,y) |
|
fxy=x+cotan(x-1/y) |
|
end function fxy |
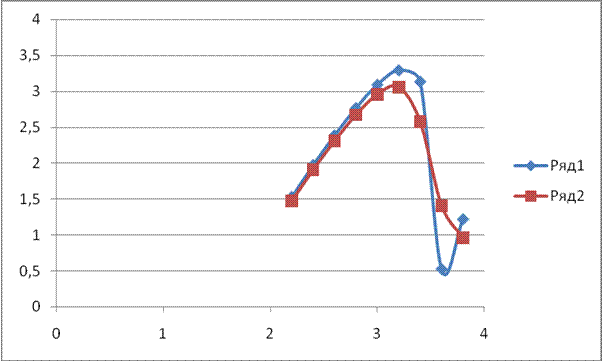
2.200000 1.528419
2.400000 1.973433
2.600000 2.386606
2.800000 2.766763
3.000000 3.090768
3.200000 3.292253
3.400000 3.133465
3.600000 0.5241269
3.800000 1.219754
2.200000 1.473591
2.400000 1.905312
2.600000 2.307181
2.800000 2.668520
3.000000 2.952698
3.200000 3.054458
3.400000 2.574191
3.600000 1.408275
3.800000 0.9586333
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КУРСОВАЯ РАБОТА
ПО ДИСЦИПЛИНЕ ИНФОРМАТИКА
для студентов 2 курса направления 280200 – защита окружающей среды
ВАРИАНТ 16
ФАКУЛЬТЕТ ЛА ПРЕПОДАВАТЕЛЬ
КОРОТАЕВАТ.А.
ГРУППА СЭ-71
Москалева Е.Е.
Новосибирск
2008
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.