Электротехника \ Электротехника

Расчет переходных процессов классическим методом в цепях первого и второго порядка (Практическое занятие № 6)

Страницы работы

32 страницы (Word-файл)
Скачать файл

Фрагмент текста работы

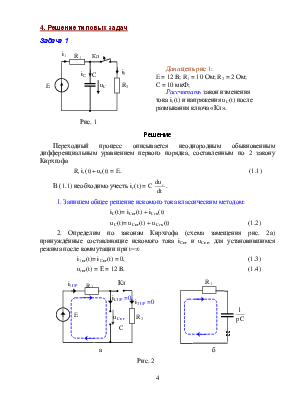
Переходный процесс описывается неоднородным обыкновенным дифференциальным уравнением первого порядка, составленным по 2 закону Кирхгофа

R1 i1 (t)+ uC(t) = E.                                                                                                                            (1.1)

В (1.1) необходимо учесть iС (t) = C .

1. Запишем общее решение искомого тока классическим методом:

iC(t)= i CПР(t) + iCСВ(t)

uC(t)= uC ПР(t) + uC СВ(t)                                                                                                                          (1.2)

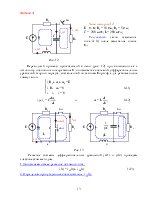
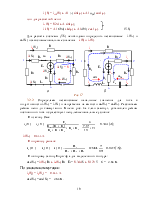
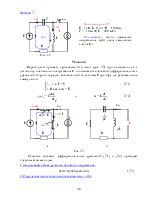
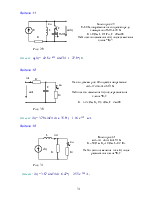
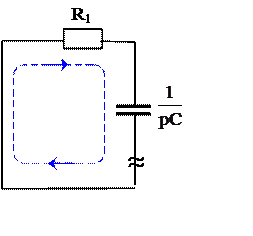
2. Определим по законам Кирхгофа (схема замещения рис. 2а) принуждённые составляющие искомого тока iСПР и uCПР, для установившимся режима после коммутации при t=∞

i 1ПР(t)= i СПР(t) = 0,                                                                                                                          (1.3)

uСПР(t) = Е = 12 B.                      (1.4)

 


а                                                                 б

Рис. 2

3. Находим свободную составляющую iСВ(t) и uC СВ(t).

Общее решение для iСВ(t) и uCСВ(t) можно записать после решения характеристического уравнения.

3.1. Составим характеристическое уравнение.

Для чего составляем схему замещения рис. 2б, относительно разрыва в любом месте после коммутационной цепи записываем входное сопротивление и,  приравнивая его нулю, получим однородное уравнение:

ZBX(р) = R1 +  = 0,                                                                                                                      (1.5)

Из 5 определим корень уравнения:      р  = –  = – 10000 =  – 104 с-1.

Определяем постоянную времени τ = 1/|p|= R1C = 10-4 с.

Записываем решение для свободной составляющей:

i ССВ(t) = Aept                и              uC СВ(t) = Bept.                                                           (1.6)

3.2. Определяем постоянные интегрирования A и B.

3.2.1. Записываем решение для тока iС(t) и напряжения uС(t) при t=0+, с учётом  (3), (4) и (6) получим:

iС(t)= i СПР(t)+ iССВ(t) = 0+ Aept,                             iС(0) = A,                                                                                    (1.7)

uC(t)= u CПР(t)+ uCСВ(t) = E + Bept,                        uС(0) = E + B =12 + B                                                                                   (1.8)

 


а                                                                 б

Рис. 3

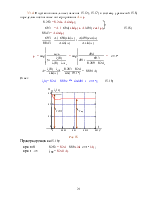
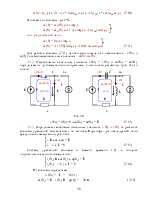
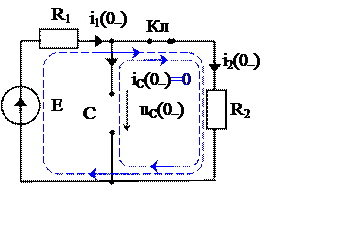
3.2.2. Определяем независимые начальные значения uC(0+) = uC(0–)

До коммутации t=0– ключ замкнут (рис. 3а.), ток в ветви с ёмкостью равен нулю и напряжение на конденсаторе равно напряжению на резисторе R2. В цепи  не нулевые начальные условия:

uC(0–) = uC(0+) = R2  = 2 B.                                                                                                                      (1.8)

3.2.3. Определяем зависимые начальные значения – iС(0+).

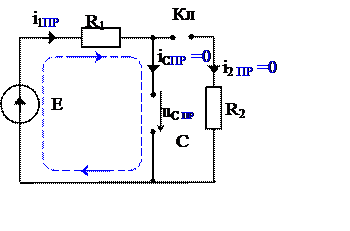
После коммутации t≥0+ ключ разомкнут (рис. 3б.), Составляем уравнение по второму закону Кирхгофа и запишем её при t = 0+:

i1 (0+) – i2 (0+) – iС (0+) = 0.

R1 i1 (0+) + uC(0+) = E.                                                                                                                            (1.9)

i2 (0+) = 0.

uC(0+) = 2 B.       i2 (0+) = 0     i1 (0+) = (E – uC(0+)) / R1 = 1 A.

i1 (0+) = iС (0+) = 1 A.                                                                                                                   (1.10)

3.2.4. Определяем постоянные интегрирования из (7) и (8) с учётом (9) и (10)

iС (0) = 0+ A = (E – uC(0+)) / R1 и            A = 1 А,                                                         (1.11) (1.13)

uC(0) = Е+ B = 0                       и            B = uC(0) – Е  = – 10 В.                                                          (1.14)

4. Записываем полное решение для рассчитываемых величин i(t) и uС(t) и строим графики процесса

iС(t) = ((E – uC(0+)) / R1 )ept =1 e–10000t А.                                                                                                                   (1.15)

uC(t)=  Е – Вept = 12 – 10 e–10000t  B.                                                                                                                              (1.16)

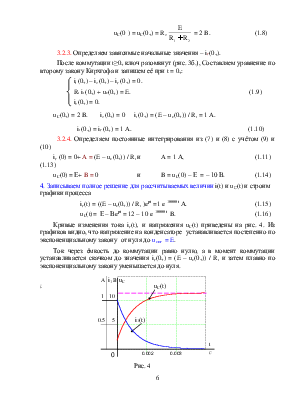
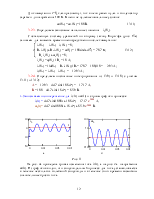
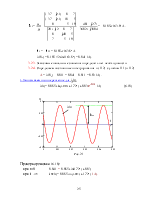
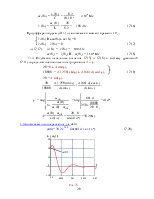
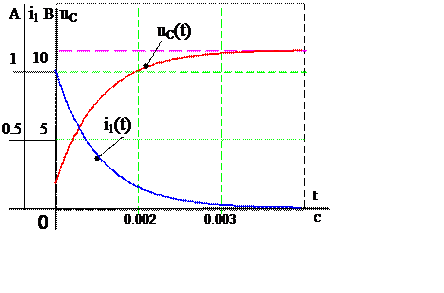
Кривые изменения тока iС(t), и напряжения uC(t) приведены на рис. 4. Из графиков видно, что напряжение на конденсаторе  устанавливается постепенно по экспоненциальному закону  от нуля до u CПР  = E.

Ток через ёмкость до коммутации равно нулю, а в момент коммутации устанавливается скачком до значения iС(0+) = (E – uC(0+)) / R1 и затем плавно по экспоненциальному закону уменьшается до нуля.

 


¿

Рис. 4

Задача 2

Дана цепь рис 5:

Е = 12 В; L = 150 мГн;

R1 = 1.2 кОм; R2 = 1.8 кОм;

Рассчитать закон изменения тока i2 (t) после замыкания ключа
 


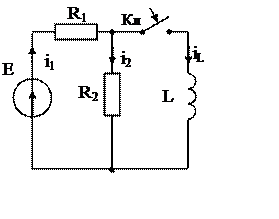Рис. 5

Решение

1.       Запишем общее решение искомого тока классическим методом:

i2(t) = i 2ПР(t)+ i2СВ(t)                                                                                                                          (2.1)

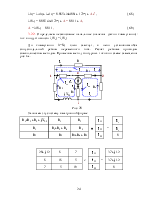
2.       Определим принуждённую составляющую искомого тока iLПР (установившийся режим после коммутации (t=∞), схема замещения рис. 6а). Из второго закона Кирхгофа:

i1ПР(t) = iLПР = Е / R1,                                                                                                                          (2.2)

i2ПР(t) = 0;

 


а                                                                 б

Рис. 6

3. Находим свободную составляющую iСВ(t) и uC СВ(t).

Общее решение для iСВ(t) и uCСВ(t) можно записать после решения характеристического уравнения.

3.1. Составим характеристическое уравнение.

Для чего составляем схему замещения цепи после коммутации рис. 6б, в которой относительно разрыва в любом месте цепи записываем входное сопротивление и,  приравнивая его нулю, получим характеристическое уравнение:

ZBX = pL + 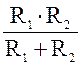 = 0,                                                                                                                      (2.3)

Из 5 определим корень уравнения:      р  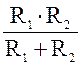= –  = – 4800с-1.                                                                          (2.4)

Определяем постоянную времени τ = 1/|p|= 2,0810-4 с.

Записываем решение для свободной составляющей:

i 2СВ(t) = Aept                                                                                                                      (2.5)

3.2. Определим постоянную интегрирования A.

 


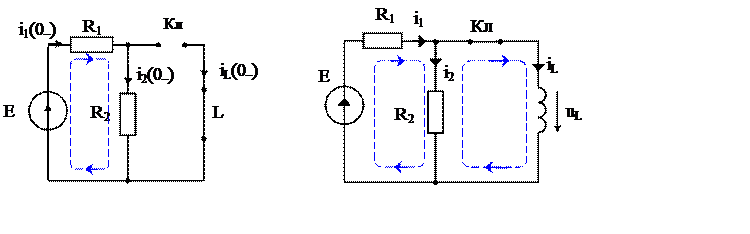а                                                                 б

Рис. 7

3.2.1. Записываем решение для тока i2(t) при t=0+, с учётом  (2.3), (2.4) и (2.6) получим:

i2(t)= i 2ПР(t)+ i2СВ(t) = 0+ Aept,                              i2(0) = A,                                                                                    (2.7)

3.2.2. Определяем независимые начальные значения iL(0+) = iL(0–).

До коммутации t=0– ключ разомкнут (рис. 6а.), ток в ветви с индуктивностью равен нулю и напряжение на конденсаторе равно напряжению на резисторе R2. В цепи  не нулевые начальные условия:

iL(0+) = iL(0–) = 0А.                                                                                                                      (2.8)

3.2.3. Определяем зависимые начальные значения – i2(0+).

После коммутации t≥0+ ключ разомкнут (рис. 6б.), Составляем уравнение по второму закону Кирхгофа и запишем её при t = 0+:

i1 (0+) – i2 (0+) – iL (0+) = 0.

R1 i1 (0+) + R2 i2 (0+) = E.                                                                                                                            (2.10)

–R2 i2 (0+) + uL(0+) = 0.

iL(0+) = 0;        i1 (0+) = i2 (0+);       i2 (0+) = E/(R1 + R2) = 4 10-3 А;                                       (2.11)

3.2.4. Определяем постоянные интегрирования из (2.7) и (2.8) с учётом (2.9) и (2.10)

i2 (0+) = 0+ A = 4 10-3         и              A = E/(R1 + R2) = 4 10-3,                                                           (12.3)

4. Записываем полное решение для рассчитываемых величин i2(t) строим графики процесса

i2(t) = (E/(R1 + R2)) ept = 4 10-3 e–4800 t А.                                                                                                                   (2.15)

 


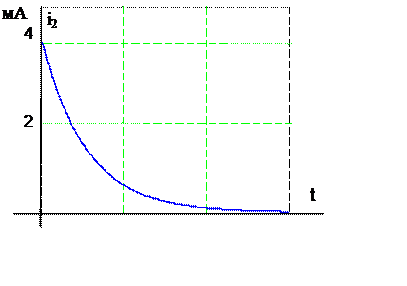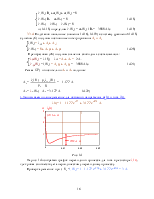
Рис. 8

Кривая изменения тока i2(t) приведены на рис. 1б. Из графиков видно, что ток в резисторе устанавливается скачком до величины 4 мА и затем постепенно по экспоненциальному закону снижается до нуля.

Задача 3

Дана цепь рис 9:

u(t) = 100sin(1000t+45o) В;

uC(0) = 100 B

R1 = R2 = 10 Ом; C = `100 мкФ;

Рассчитать закон изменения тока iC (t) и напряжения uC(t) после замыкания ключа
 
 


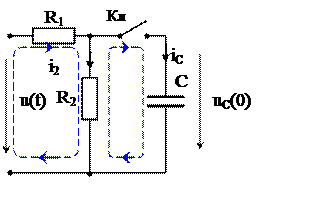Рис. 9

Решение

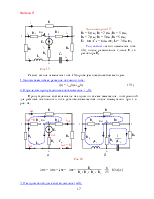
Переходный процесс в цепи рис 9 после замыкания ключа описывается системой неоднородных обыкновенных дифференциальных уравнений первого порядка, составленных по законам Кирхгофа

i1 (t) –   i2 (t) – iС (t) = 0.

R1 i1 (t)+ R2 i2 (t) = u(t) = 100sin(1000t+45o) В.                                                                                                                            (3.1)

– R2 i2 (t) +uC(t) =0.

В (1) необходимо учесть iС (t) = C .

1. Запишем общее решение для искомого тока и напряжения классическим методом:

iC (t)= i CПР(t)+ iCСВ(t)  и        uC(t)= u CПР(t)+ uCСВ(t)                                                               (3.2)

 


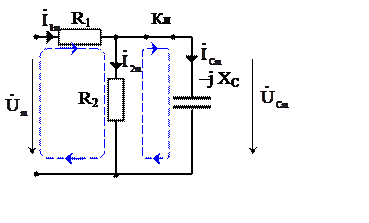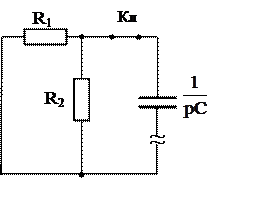а                                                                 б

Рис. 10

2. Определим принуждённую составляющую искомого тока iCПР(t) и напряжения uCПР(t) в установившемся синусоидальном режиме после коммутации (t = ∞). Применим символический метод расчета. На рис. 6а приведена схема замещения для расчёта цепи в установившемся синусоидальном режиме после коммутации (t=∞).

·  Комплекс амплитудного значения питающего напряжения:

 = Um ejΨ = 100 ej45 B.

Ÿ  Емкостное сопротивление:

XС =  =  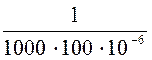= 10 Ом.

Ÿ  Комплексное входное сопротивление:

Z = R1 + 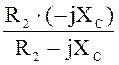 = 10 +  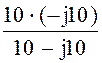= 15 – j5 Ом.

Ÿ  Комплекс амплитудного значения входного тока:

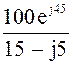 =  =  = 2.83 + j 5.66 = 6.32Ð63.4° A.

Ÿ  Комплекс амплитудного значения напряжения на ёмкости:

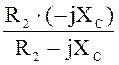 =   = 6.32Ð63.4° (5 – j5) = 42.4+j14.1 = 44.7Ð18.4° B.

Ÿ  Комплекс амплитудного значения тока через ёмкость:

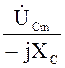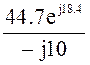 =  =  =  – 1.41+j4.24 = 4.47Ð108.4° B.                                                                                                                    (3.7)

Ÿ  Мгновенные значения тока через ёмкость:

i СПР(t) = 4.47 sin(1000t + 108.4°) А.                                                                                                                      (3.7)

Ÿ  Мгновенные значения принуждённого напряжения на ёмкости:

u СПР(t) = 44.7 sin(1000t + 18.4°) В.                                                                                                                      (3.7)

3. Определим свободную составляющую тока через ёмкость

Похожие материалы

Информация о работе

ВУЗ:
Новосибирский государственный технический университет (НГТУ)
Предмет:
Электротехника
Тип:
Методические указания и пособия
Категория:
Электротехника (Технические предметы)
Размер файла:
940 Kb
Скачали:
0
Скачать файл