Автоматизированный электропривод подъемной тележки

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Кафедра ЭАПУ

Расчетно-графическая работа

по дисциплине

«Электромеханические системы»

на тему

«Автоматизированный электропривод подъемной тележки»

Факультет:	МТ
Группа:	КП-02
Студент:	Андросенко Ю.А.
Преподаватель:	Путинцев Н.Н.

Вариант 1- 10

Новосибирск – 2003г.

                                           Исходные данные

Кинематическая схема привода приведена на рис.1.

Рис.1. Кинематическая схема механизма:  1 – двигатель;     2 – редуктор;   3 – барабан;    4 – тележка.

                    

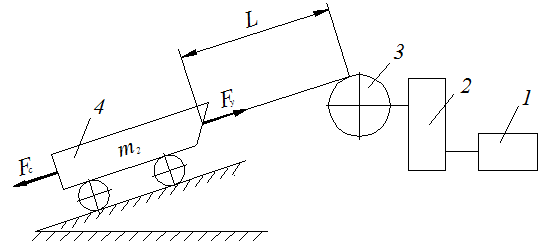
Технические данные к механизму подъемной лебедки:

Масса груженой тележки	m2, т	12
Сила статического сопротивления	Fс, кН	10
Диаметр активного сечения каната	dк,10-3м	22
Длина активного сечения каната	Lк, м	40
Площадь активного сечения каната	Sк, 10-4м2	1,85
Диаметр барабана	Дб, м	0,5
Момент инерции барабана	Jб, кг×м2	60
Передаточное число редуктора	i	40
Зазор, обусловленный провисанием каната перед началом движения	Zx, 10-3м	10

Технические данные схемы электропривода:

Номинальные параметры двигателя	Рн, кВт	12
	Uн, В	220
	nн, об/мин	1060
	Iн, А	63
	Rя, Ом	0,24
Момент инерции двигателя	Iд, кг×м2	0,25
Коэффициент усилия	КП	35
Постоянная времени преобразователя	Тm, 10-2с	1
Суммарное сопротивление якорной цепи	Rå, Ом	0,4
Электромагнитная постоянная времени	Тя, с	0,1

Расчет параметров регуляторов системы подчиненного регулирования

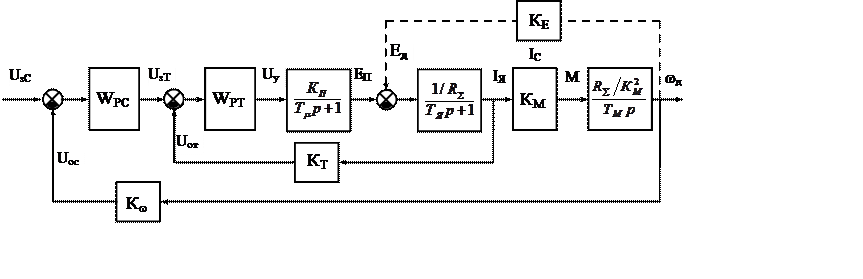На рис. 2 показана  структурная схема электропривода.

Рис. 2. Структурная схема электропривода

Характер переходного процесса можно описать  системой  уравнений движения:

;

;

.

На начальной стадии проектирования электромеханической системы предполагают, что все звенья кинематической  цепи связаны жестко и нет никаких зазоров в зацеплениях.

Параметры рассчитываются из закона сохранения энергии. 

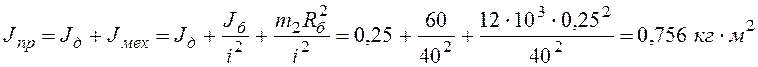  –  приведенный момент инерции;

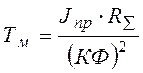– электромеханическая постоянная времени;

где КФ – коэффициент пропорциональности между ЭДС и скоростью w, рассчитывается из электромеханической характеристики:

;

;

.

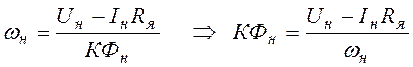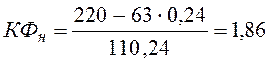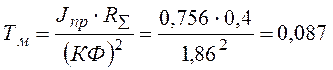
Принимаем ; U_{ЗТ max} = 10 В, U_{Зw max} = 10 В – максимальные значения тока, задающих напряжений на контур тока и скорости. К_Е = К_М = КФ = 1,86.

В соответствии с методикой синтеза системы подчиненного регулирования тока с настройкой   на   технический  оптимум   передаточные   функции   регуляторов   определяются выражениями:

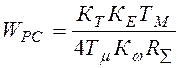–  передаточная функция регулятора скорости;

Значения коэффициентов обратных связей по току и скорости определяем из отношений

;      .

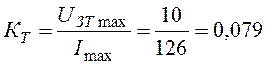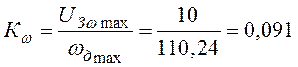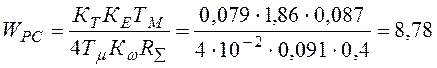
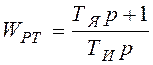 – передаточная функция регулятора тока, где    Т_Я – электромагнитная постоянная времени;

.

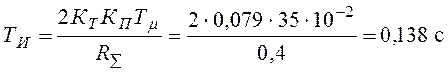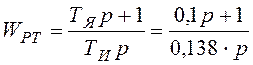
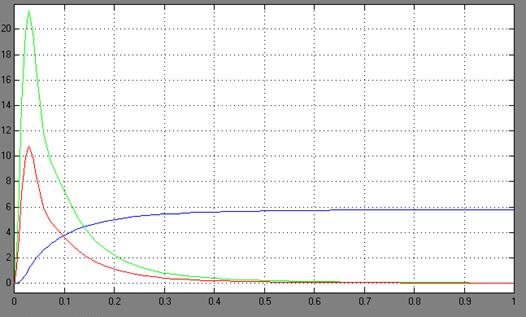
Рис. 3. – ПП по скорости, моменту и току при входном напряжении 1 В, время моделирования 1 с

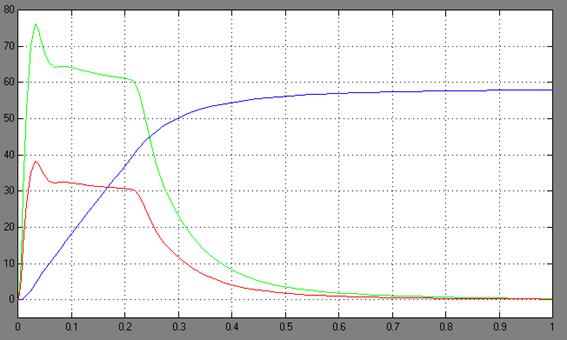
Рис. 4. – ПП по скорости, моменту и току при входном напряжении 10 В, время моделирования 1 с.

Математическая модель и структурная схема механизма

Для анализа динамических характеристик производственного механизма предварительно составляем его расчетную схему и определяем ее параметры. Расчетная схема отражает наличие зазоров и упругих звеньев в кинематических связях между элементами (массами) механизма. Значения параметров расчетной схемы (масс, сил, моментов, коэффициентов жесткости, величины зазора) приводим к движению одного из элементов механизма – вращательному движению со скоростью w₂ барабана.

 

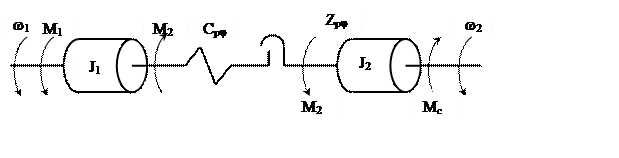Рис. 5. Расчетная схема механизма

Параметры расчетной схемы, приведенные к оси вращения барабана, вычисляются по соотношениям:

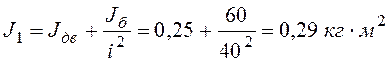 – приведенный момент инерции двигателя и барабана;

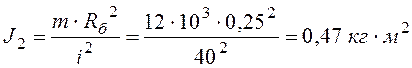– приведенный момент инерции тележки; 

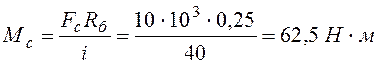 – момент сопротивления;

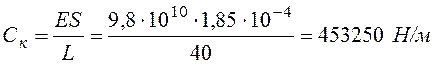 – коэффициент жесткости, где  – модуль упругости первого рода;

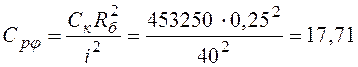– расчетный коэффициент жесткости каната;

;

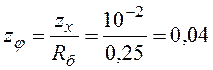– величина зазора.

 

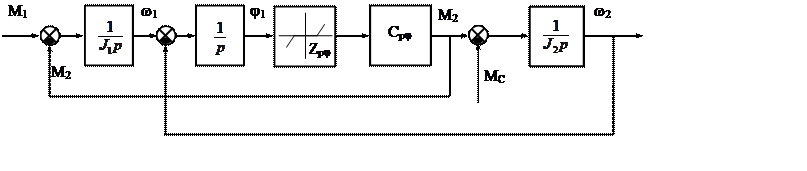Рис. 6. Структурная схема механизма

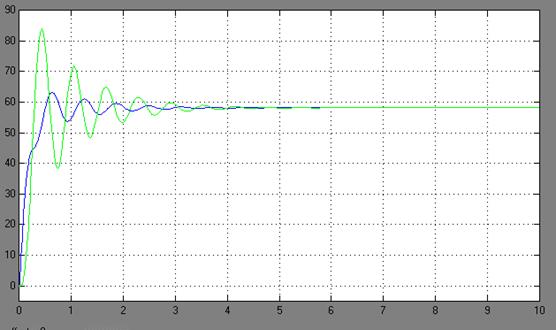
Рис. 7. – ПП по скорости механизма и тележки. Двухмассовая модель без зазора, входное напряжение 10 В, время моделирования 10 с

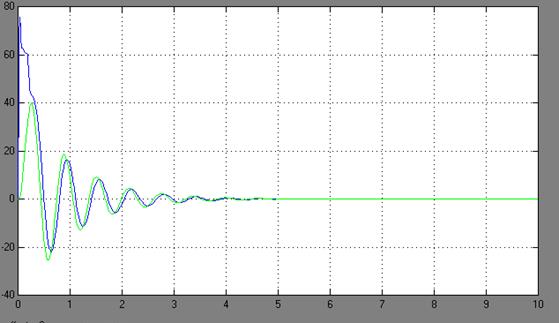
Рис. 8. – ПП по моменту механизма и тележки. Двухмассовая модель без зазора, входное напряжение 10 В, время моделирования 10 с

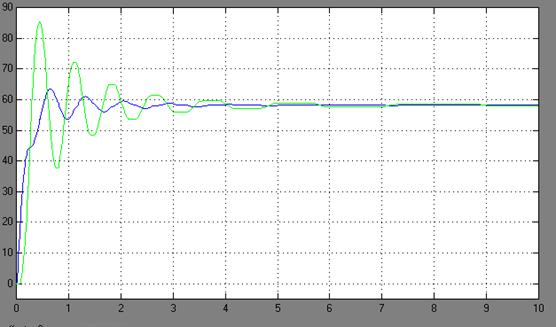
Рис. 9. – ПП по скорости механизма и тележки. Двухмассовая модель с зазором, входное напряжение 10 В, время моделирования 10 с

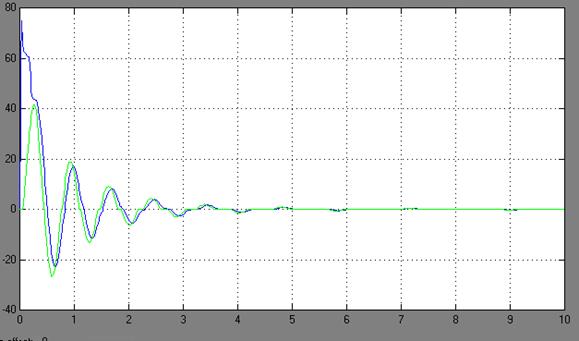
Рис. 10. – ПП по моменту механизма и тележки. Двухмассовая модель с зазором, входное напряжение 10 В, время моделирования 10 с

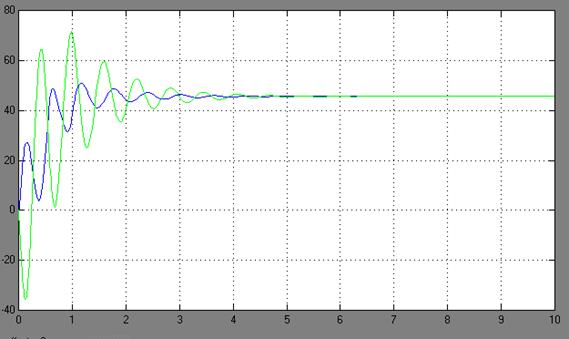
Рис. 11. – ПП по скорости механизма и тележки. Двухмассовая модель с зазором и моментом сопротивления М_с, входное напряжение 10 В,  время моделирования 10 с

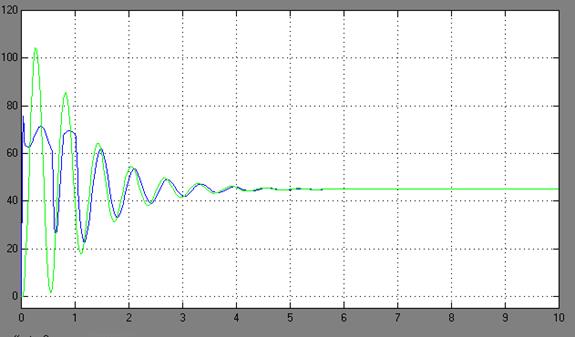
Рис. 12. – ПП по моменту механизма и тележки. Двухмассовая модель с зазором и моментом сопротивления М_с, входное напряжение 10 В, время моделирования 1,2 с

Выводы

При рассмотрении графиков переходных процессов электромеханической системы можно увидеть, что по сравнению с одномассовой моделью (идеализированной), которая имеет плавные не колебательные переходные процессы, двухмассовая модель (реальная) имеет колебательный переходной процесс. Это обусловлено тем, что двухмассовая модель предусматривает наличие упругой нежесткой связи, зазора и момента сопротивления.   На графиках переходных процессов системы с наличием зазора колебания происходят с задержкой по времени, то есть на данных временных промежутках происходит «выборка»  зазора. Причем, с учетом момента сопротивления амплитуда и частота колебаний возрастает, что ведет к ухудшению переходного процесса.

Для стабильной работы системы вводим ограничение по току, которое предохраняет систему от возрастания тока больше его предельного значения.

Предложенный метод синтеза регуляторов скорости и тока нас не удовлетворяет т.к. система находится на границе устойчивости. Для решения этой проблемы необходимо применять другие методы синтеза.