Реализация случайных процессов. Оценка средних по времени математического ожидания и дисперсии, страница 2

1

0,831935

0,692112

0,575797

0,479026

0,398519

0,331542

0,276373

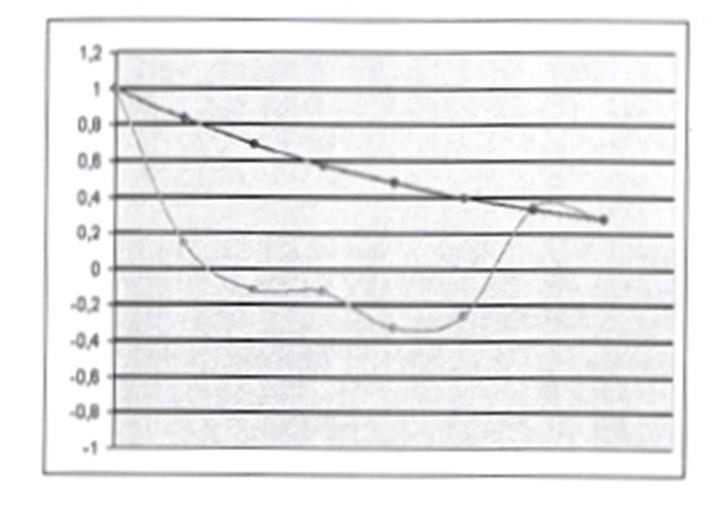
Функция имеет вид 

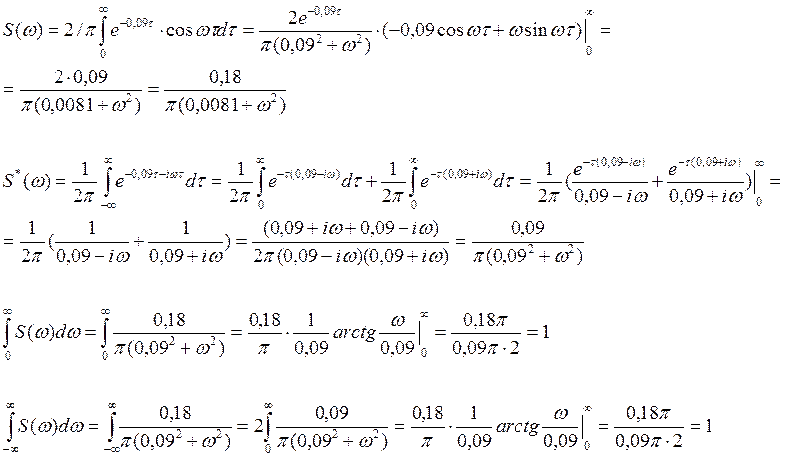
Графики:

Задание по КП, курс «ТВ, МС и СП» «СГМ»

Задание.

Случайный процесс (СП) задан совокупностью n реализаций в m сечениях по t и t₀=0. Исходные данные поясняет рис. 1

Рис.1. Представление реализаций СП, принять n=10,…,14,    m=14,…,20.

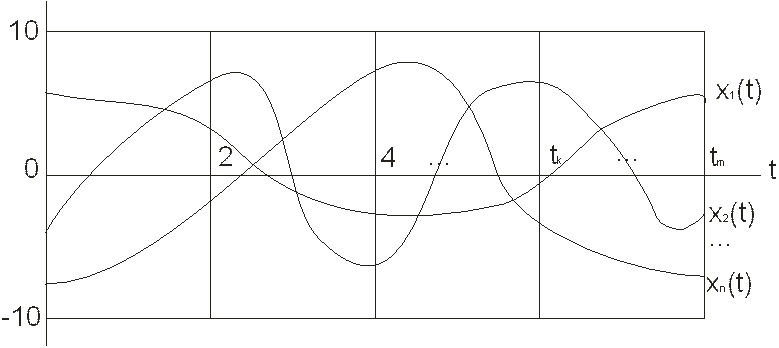
Замечание.

Данные из рис.1 удобно представить таблицей в виде

Таблица 1

	0	2	…	tk	…	tm
1	x1(t0)	x1(t2)	…	x1(tk)	…	x1(tm)
…
i	xi(t0)	xi(t2)	…	xi(tk)	…	xi(tm)
…
n	xn(t0)	xn(t2)	…	xn(tk)	…	xn(tm)

Приведённые данные используются в последующих расчетах и только они.

Необходимо:

1. Оценить m_x(t) и представить графически на рис.1 и в виде таблицы по сечениям.

Расчетная формула:

2. Оценить D_x(t) и представить результаты в виде таблицы по сечениям, причем

3. Привести СП x(t) к стационарному, т.е оценить средние по времени математическое ожидание и дисперсию, обозначая их соответственно  и .

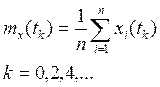
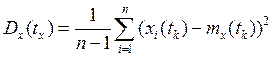
Рассчитать σ_x(t_k) и представить в виде таблицы по сечениям, полагая

4. Рассчитать корреляционные моменты по формуле

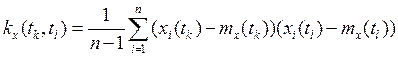
и представить результаты в виде таблицы 2

Таблица 2

t´                       t	0	2	…	tm
0	D0	k02		k0m
…
tm				Dm

Замечание: Из теории известно, что для стационарного процесса k(t,t´)=k(t´,t)=k(τ), т.е таблица 2 содержит одинаковые по величине симметричные элементы.

5. Нормировать оценки корреляционных моментов, приведенных в таблице 2, т.е необходимо разделить значения оценок на произведения соответствующих средних квадратических отклонений. Результаты расчетов представить таблицей (типа таблицы 2).

6. Осреднить оценки нормированной корреляционной функции и результаты представить таблицей по сечениям, обозначая оценки ρ_x(τ), и в виде точек на графике (число точек должно быть равно числу сечений).

7. Построить непрерывный вид ρ_х(τ), используя методы приближения, например ρ_х(τ)=a₀+a₁τ, а оценки a₀ и a₁ найти по методу наименьших квадратов.

Замечание: Часто оказывается полезной функция вида

8. Построить график S_x(ω) нормированной спектральной плотности, используя преобразование

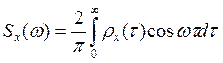
Найти значение функции S_x(ω) при ω=0.

Проверить результат, используя равенство вида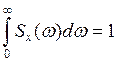

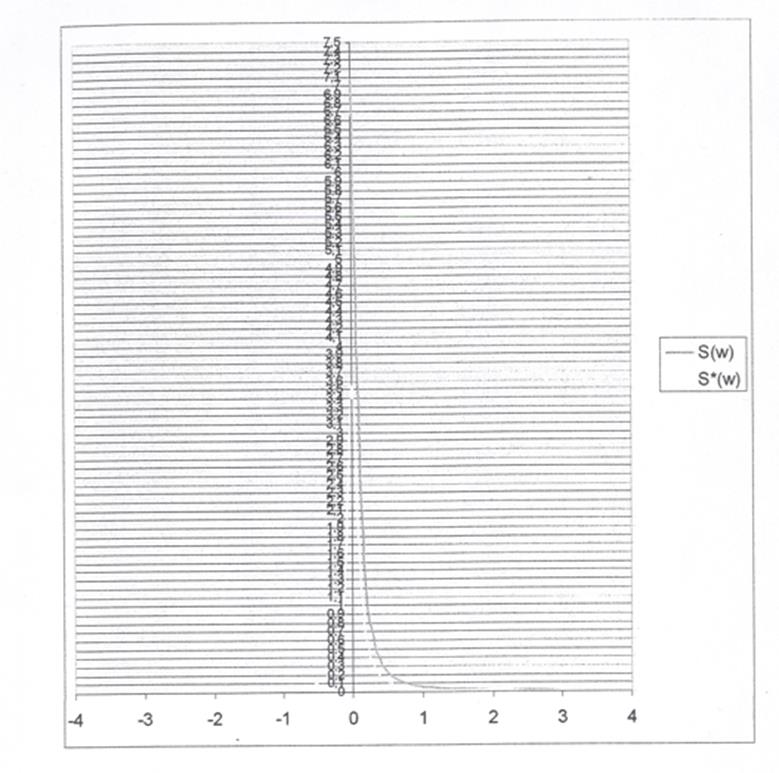
Построить график S_x(ω)

9. На полученный график нанести график функции S_x^*(ω), используя преобразование

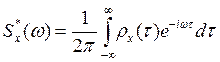
Найти значение S_x^*(0).

S_x^*(ω) – нормированная спектральная плотность в комплексной форме.

Сравнить графики и сделать выводы.

Литература:

Вентцель Е.С. Теория вероятностей. М.,1969

Министерство общего профессионального образования РФ

Новосибирский Государственный Технический Университет

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

по теории вероятностей и математической статистике

Новосибирск

2003

Реализация случайных процессов:

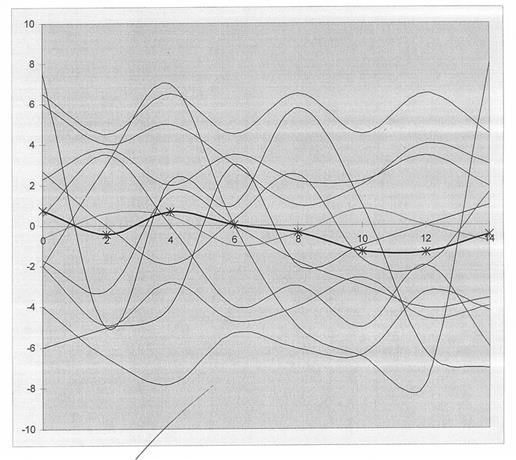
Таблица экспериментальных данных:

N\t	0	2	4	6	8	10	12	14
1	-6	-5	-4	3	-2	-1	0	1
2	6	4	5	3	1	2	4	3
3	0,5	3,5	0	-4	-3	-5	-2	-6
4	-2	3	7	0	-5	-6,5	-7,8	8
5	-2	-4,9	-2,8	-4,7	-4	-2,6	-4,6	-4
6	-1,7	-3,2	1,7	0	-1,8	-3	-4,1	-3,6
7	-0,6	0,6	0,5	-1	-0,4	0,8	0	-0,8
8	7,5	-5	2,2	1	5,8	1	-6,3	-7,1
9	2,7	0	-1,9	0,3	2,5	-1,7	-2	1,6
10	2,3	3,8	2	3,5	2,2	2,2	3,4	1,9
11	-4	-6,5	-7,8	-5,3	-6,1	-6,4	-3,3	-4,2
12	6,5	4,5	6,5	4,5	6,5	4,5	6,5	4,5