Решение нелинейных алгебраических уравнений и их систем

Лабораторная работа №2

Решение нелинейных алгебраических уравнений и их систем

Студент                     Кохно

Группа                       РМС7-71

Преподаватель          Лобыч

Вариант                     9

Задание 2

Построить графики левых частей следующих уравнений на заданном интервале (по вариантам). Убедиться в наличии корней и определить их нулевые приближения по графику.

Код главной функции:

// Программа для расчета графика функции

#include "datafile.h"

double F(double); // прототип отстраиваемой функции

void main()

{

// описание данных

     int Npnt,keyDemo;

     double Xmin,Xmax;

// ввод входных данных

     Xmin=2;

     Xmax=5;

     Npnt=100;

     keyDemo=1;

// расчет и вывод выходных данных в файл

     WriteFunc(F,Xmin,Xmax,Npnt,keyDemo);

}

#include <math.h>

double F(double x)

{

  return exp(0.2*x)*(pow(sin(x-1),2)+cos(-x));

Полученый график:

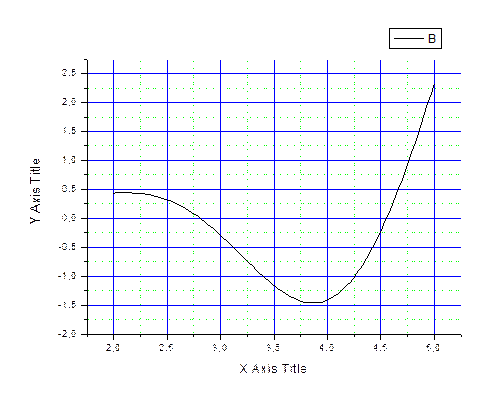
Нулевые приближения: X=4.7 и X=2.5 использованы в задании 3

Задание 3

Методом Ньютона найти значения всех корней на заданном интервале с точностью . Один из корней вычислить методами простых итераций и бисекции. Для этого корня сохранить и привести в отчете данные итераций.

Примечание:

Главная функция в файле ROOT02

Код главной функции:

#include <iostream.h>

#include <conio.h>

#include "root.h"

double F(double);

void main()

{

// описание данных

int Nckl,Err;

double epsX,epsF,X,Fx,DX;

// ввод входных данных

epsX=1E-08;

epsF=1E-08;

X=4.7;

// решение

clrscr();

cout<<"1-е решение методом Ньютона"<<endl;

Err=RootNewton(F,epsX,epsF, X, Fx,Nckl,3);

// вывод результата

cout<<endl<<endl;

cout<<" Err = "<<Err<<endl;

cout<<"   X = "<<X<<endl;

cout<<" 2 Fx = "<<Fx<<endl;

cout<<"Nckl = "<<Nckl<<endl;

cout<<endl<<"2-е решение методом Ньютона:";

X=2.5;

Err=RootNewton(F,epsX,epsF, X, Fx,Nckl,3);

// вывод результата

cout<<endl<<endl;

cout<<" Err = "<<Err<<endl;

cout<<"   X = "<<X<<endl;

cout<<" 2 Fx = "<<Fx<<endl;

cout<<"Nckl = "<<Nckl<<endl;

getch();

//Решение медодом простых итераций

DX=0;

Nckl=0;

RootSimpIt(F,epsX, X,DX,Nckl);

cout<<endl<<endl;

cout<<"X="<<X;

getch();

//Решение методом половинного деления

double A,B;

A=2.5;

B=3.5;

RootBisecty(F,A,B,epsX,epsF,X,Fx,Nckl);

cout<<endl<<"Ответ метод половинных делений"<<endl<<"X="<<X;

getch();

}

#include <math.h>

double F(double x)

{

return exp(0.2*x)*(pow(sin(x-1),2)+cos(-x));

}

Вывод:

Программа выдает одинаковые корни во всех методах.Значит работает она правильно

Задание 4

С помощью RootNewton() или RootBisecty() (по указанию преподавателя) найти первый положительный корень уравнения , где  - функция Бесселя n-го порядка. Значение  взять по вариантам: 3, 4, 5, … и т.д. и обеспечить его передачу в функцию левой части уравнения через глобальную переменную. В этой левой части уравнения использовать функцию bessj() из модуля bessj.cpp.

Примечание: запускается с помощью файла График/GRAPHIC1.cpp и Решение/Root2.cpp

Код исполняемой функции для графика:

// Программа для расчета графика функции

#include "datafile.h"

int n=9;

double F(double); // прототип отстраиваемой функции

double bessj(int,double);

void main()

{

// описание данных

     int Npnt,keyDemo;

     double Xmin,Xmax;

// ввод входных данных

     Xmin=0;

     Xmax=20;

     Npnt=100;

     keyDemo=1;

// расчет и вывод выходных данных в файл

     WriteFunc(F,Xmin,Xmax,Npnt,keyDemo);

}

#include <math.h>

double F(double x)

{

  return bessj(n,x);

}

График:

Файл Home.dat

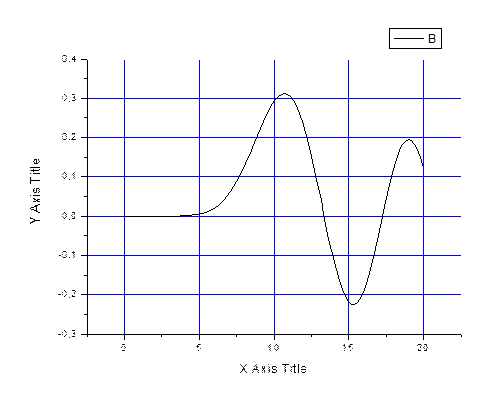
Из графика видны нулевые приближения

Управляющая функция для отыскивания корня:(Файл Root2.cpp)

#include <iostream.h>

#include <conio.h>