Решение нелинейных алгебраических уравнений и их систем, страница 2

#include "root.h"

#include <math.h>

double bessj(int,double);

int n=9;

double F(double);

void main()

{

// описание данных

int Nckl,Err;

double epsX,epsF,X,Fx;

// ввод входных данных

epsX=1E-08;

epsF=1E-08;

X=12.5;

// решение

clrscr();

cout<<"бессель 9 порядка 1-й корень методом Ньютона:"<<endl;

Err=RootNewton(F,epsX,epsF, X, Fx,Nckl,3);

// вывод результата

cout<<endl<<endl;

cout<<" Err = "<<Err<<endl;

cout<<"   X = "<<X<<endl;

cout<<"  Fx = "<<Fx<<endl;

cout<<"Nckl = "<<Nckl<<endl;

getch();

}

double F(double X)

{

return bessj(n,X);

}

Примечание: использовано нулевое приближение Х=12.5 и прорешено методом ньютона

Вывод:

Из построенного графика следует, что найденный корень Х=13.3543 соответствует действительному.

Задание 5

C помощью RootNewton() или RootBisecty() (по указанию преподавателя) найти первый положительный корень уравнения F(x) = 0, где левая часть уравнения реализована в виде неизвестной подпрограммы – функции с заголовком   double F(double x) и находящейся в файле f*.obj (по вариантам). Указание: Этот файл следует объединить в проект вместе с управляющей программой и файлом root.cpp. Предварительно следует построить график левой части уравнения и выбрать нулевое приближение или интервал поиска корня.

График (Graphick1.cpp)

// Программа для расчета графика функции

#include "datafile.h"

doubleF(double); // прототип отстраиваемой функции

voidmain()

{

// описание данных

intNpnt,keyDemo;

doubleXmin,Xmax;

// ввод входных данных

Xmin=0;

Xmax=5;

Npnt=100;

keyDemo=1;

// расчет и вывод выходных данных в файл

WriteFunc(F,Xmin,Xmax,Npnt,keyDemo);

}

#include <math.h>

При подключении функции получили следующий график:

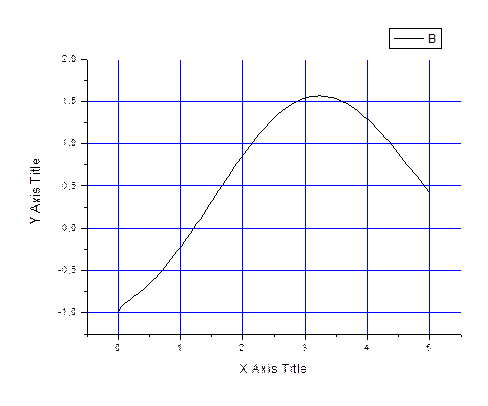
Из графика следует что нулевое приближение можно взять равным 0.5

Программа для подсчета корня:

#include <iostream.h>

#include <conio.h>

#include "root.h"

#include <math.h>

double F(double);

void main()

{

// описание данных

     int Nckl,Err;

     double epsX,epsF,X,Fx;

// ввод входных данных

     epsX=1E-08;

     epsF=1E-08;

     X=0.5;

// решение

     clrscr();

     cout<<"Первый полож. корень методом Ньютона:"<<endl;

Err=RootNewton(F,epsX,epsF, X, Fx,Nckl,3);

// вывод результата

     cout<<endl<<endl;

cout<<" Err = "<<Err<<endl;

     cout<<"   X = "<<X<<endl;

cout<<"  Fx = "<<Fx<<endl;

     cout<<"Nckl = "<<Nckl<<endl;

     getch();

}

Рассчет корня произведен методом ньютона.

Вывод: Очевидно что корень уравнения равный 1.214786 соответствует действительности

Задание 7

С помощью RootSysNewton()решить одну из следующих систем (по вариантам):

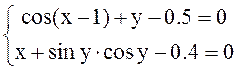
Управляющая программа:

#include <iostream.h>

#include <conio.h>

#include "root.h"

int Systema(Vector X, Vector F);

void main()

{

// описаниеданных

     int n,Nckl,Err;

     double epsX,epsF,IDXI,IFxI;

Vector X,Fx;

// ввод входных данных

n=2;

     epsX=epsF=1E-08;

     X[1]=10;

X[2]=10;

// решение

     clrscr();

     Err=RootSysNewton(Systema,n,epsX,epsF,X,Fx,IDXI,IFxI,Nckl,3);

// вывод результата

     cout<<endl;

     cout<<"  Err = "<<Err<<endl;

cout<<" X[1] = "<<X[1]<<endl;

     cout<<" X[2] = "<<X[2]<<endl;

     cout<<endl;

     cout<<"Fx[1] = "<<Fx[1]<<endl;

     cout<<"Fx[2] = "<<Fx[2]<<endl;

     cout<<endl;

     cout<<" IDXI = "<<IDXI<<endl;

     cout<<" IFxI = "<<IFxI<<endl;

     getch();

}

#include <math.h>

int Systema(Vector X, Vector F)

{

   F[1]=cos(X[1]-1)+X[2]-0.5;

   F[2]=X[1]+sin(X[2])*cos(X[2])-0.4;

return 0;

}

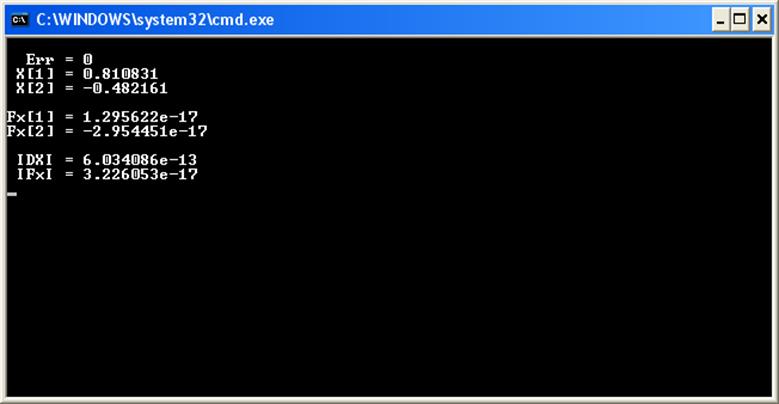
Ответ: