





Моделирование сопротивлений диффузионных и ионнолегированых слоев.
Диффузия может быть общей и локальной, в первом случае она осуществляется по всей поверхности подложки, а во втором на определенных участках пластины через специально сделанные окна маски.
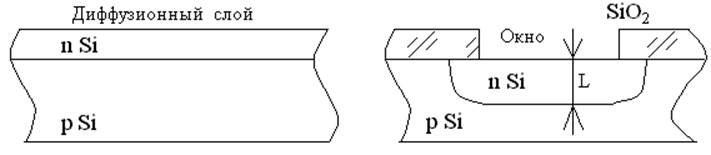
Общая диффузия приводит к образованию тонкого эпитаксиального слоя на поверхности подложки, имеющий постоянный профиль. При осуществлении диффузии через окно маски распределение примеси по глубине будет не однородным.
1). Одноэтапная диффузия.
Профиль распределения примеси по глубине:
![]() , где
, где ![]() – доноры или акцепторы,
– доноры или акцепторы, ![]() –характеристическая
длина:
–характеристическая
длина:
![]() , где t– время,
, где t– время, ![]() температурная
зависимость коэффициента диффузии:
температурная
зависимость коэффициента диффузии:
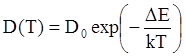
![]() – дополнительная функция ошибок.
– дополнительная функция ошибок.
2). Двух этапная диффузия(загонка-разгонка).
Гауссово распределение примеси по глубине:
![]() , где
, где ![]() – доноры или акцепторы,
– доноры или акцепторы, ![]() –характеристическая
длина:
–характеристическая
длина:
3). Ионное легирование
Гауссов профиль распределения примеси со смещенной координатой:
![]()
Задание:
Металлургическая граница p-n
перехода ![]() в кремниевой структуре с диффузионным
слоем определяется из уравнения:
в кремниевой структуре с диффузионным
слоем определяется из уравнения:
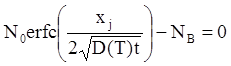 , (1)
, (1)
где 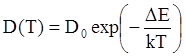
|
Диффузант |
|
|
|
B |
0.555 |
3.42 |
Построить явную программную
модель, описывающую зависимость ![]() .
.
Рассчитать зависимости ![]() в диапазонах аргумента и при значениях
параметров, указанных в следующей таблице.
в диапазонах аргумента и при значениях
параметров, указанных в следующей таблице.
|
Вариант |
Диффузант |
|
|
|
|
|
7 |
B |
5.1019 |
1.1016 |
900 … 1250 |
120 |
Достроить модель, чтобы она рассчитывала еще и удельное поверхностное сопротивление слоя:
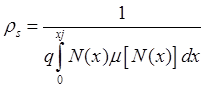 , где
, где ![]() - эффективная концентрация примеси:
- эффективная концентрация примеси:
![]() , а
, а ![]() - подвижность основных носителей заряда.
- подвижность основных носителей заряда.
Зависимость ![]() рассчитывать по формуле Зильбергера для Т
= 300 К.
рассчитывать по формуле Зильбергера для Т
= 300 К.
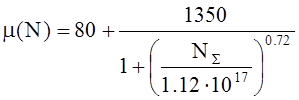 для электронов и
для электронов и
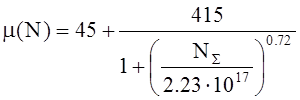 для дырок.
для дырок.
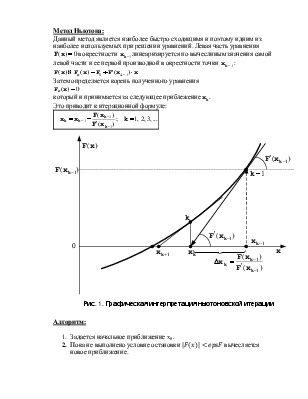
Для определения глубины залегания металлургической границы решалось уравнение (1) методом Ньютона.
Метод Ньютона:
Данный метод является
наиболее быстро сходящимя и поэтому идним из наиболее используемых при решении
уравнений. Левая часть уравнения ![]() в окрестности
в окрестности ![]() линеаризируется по вычеслиным значения самой левой
части и ее первой производной в окрестности точки
линеаризируется по вычеслиным значения самой левой
части и ее первой производной в окрестности точки ![]() :
:
![]()
Затем определяется корень полученного уравнения
![]()
который и принимается за
следующее приблежение![]() .
.
Это приводит к итерационной формуле:
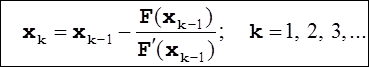
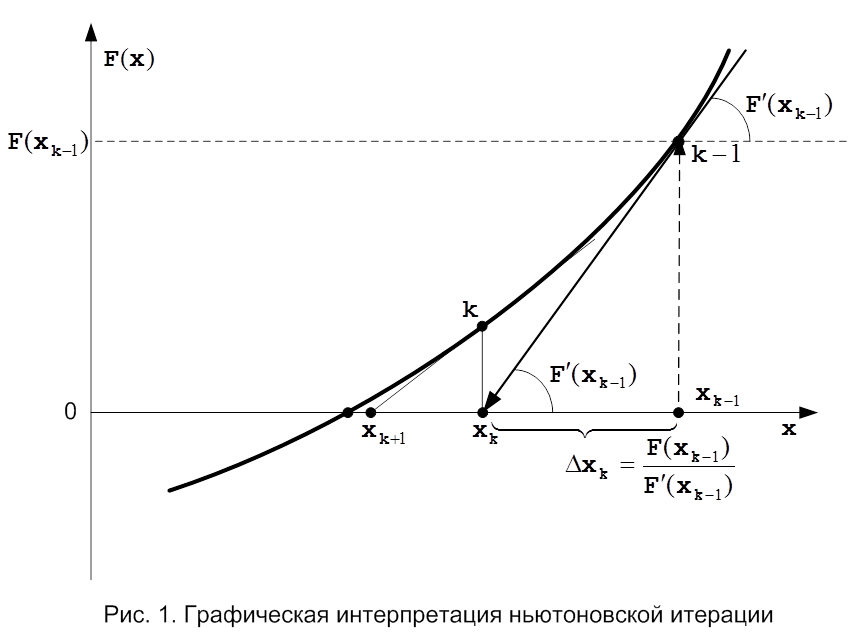
Алгоритм:
1. Задается начальное приближение x0.
2.
Пока не выполнено условие
остановки ![]() вычесляется
новое приближение.
вычесляется
новое приближение.
Метод Ньютона в классическом варианте не всегда сходится. Итерации сходятся к значению корня лишь тогда, когда на их интервале знаки первой и второй производных от левой части уравнения не изменяются. Для других случаев существуют специальные разновидности метода Ньютона с более сложными алгоритмами.
Программа для расчета металлургической границы p-n перехода и удельного поверхностного сопротивления:
//функции расчета металлургической границы и удельного сопротивления
//легированного бором
#include <conio.h>
#include <iostream.h>
#include <math.h>
#include "root.h"
#include "integral.h"
double erfc(double z);//функция ошибок
double N (double xj);
double Conductivity(double x);
double Nv_, No_, T_, t_; //глобальные переменные
void xj(double Nv, double No, double T, double t, double &xj, double &ros)
{
double epsX, epsF, X, Fx;
int Nckl, Err;
//подключение глобальных переменных
Nv_=Nv;
No_=No;
T_=T+273; //температура [K]
t_=t;
epsX=1E-10; //нулевsе приближения для метода Ньютона
epsF=1E+4;
xj=0;
Err=RootNewton(N, epsX, epsF, xj, Fx, Nckl);
if(Err!=0)
{
xj=0;
ros=0;
}
//расчёт ros
ros=1/SdxSimps(Conductivity, 0, xj, 1000);
xj=1E+04*xj;
}
double N(double xj)
{
double k,dE,Do,Dt;
k=8.61738E-5; //постоянная Больцмана [эВ*K^-1]
dE=3.42; //ширина запрещенной зоны Бора
Do=0.555; //[(м^2)/с]
Dt=Do*exp(-(dE/(k*T_))); //температурная зависимость коэффициента диффузии
return No_*erfc(xj/(2*sqrt(Dt*t_)))-Nv_;
}
double Mobility(double N) //подвижность для дырок по модели Зильбергера
{
return 45+415/(1+pow((N+2*Nv_)/2.23E+17,0.72));
}
double Conductivity(double x) //удельная проводимость кремния
{
double q = 1.6E-19;
return q*Mobility(N(x))*N(x);
}
Управляющая программа для проверки расчета металлургической границы и построения температурной зависимости Xj(T):
#include <iostream.h>
#include <conio.h>
#include "datafile.h"
#include <math.h>
#include "define.h"
#include "root.h"
#include <stdio.h>
//программа для получения температурной зависимости
//металлургического перехода
void xj(double Nv,double No,double T,double t, double &xj, double &ros);
{
double No, Nv, t, T0, Xj, ROS;
LVector T,Y;
int i;
No=5E+19;
Nv=1E+16;
T0=900;
t=7200;
for (i=0;i<=10;i++)
{ T[i]=T0+i*35;
xj(Nv,No,T[i],t,Xj,ROS);
Y[i]=Xj;
}
Write2Vec(0,10,T,Y);
}
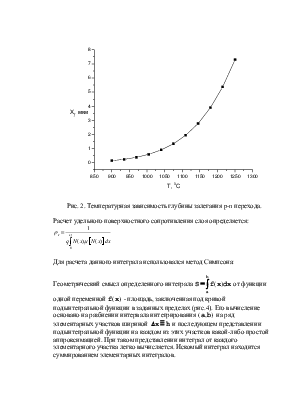
При температуре T=11250C:
Xj=2.2764 мкм.
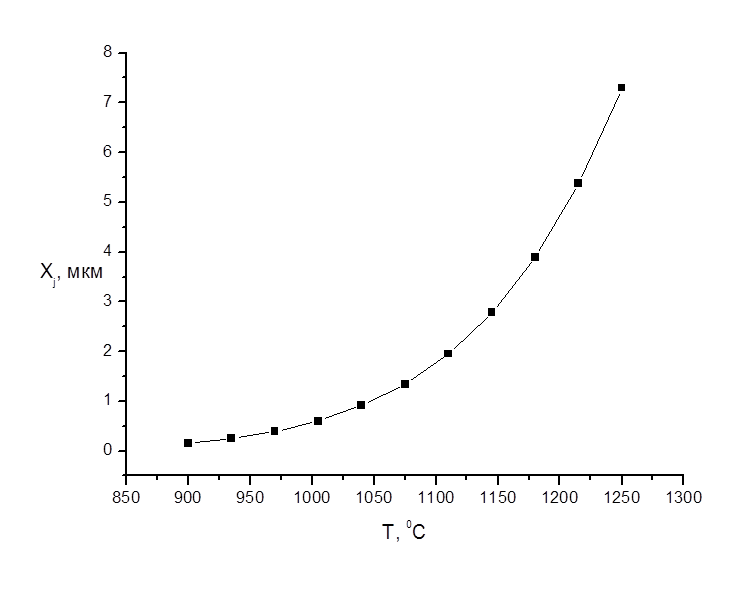
Рис. 2. Температурная зависимость глубины залегания p-n перехода.
Расчет удельного поверхностного сопротивления слоя определяется:
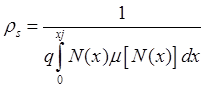
Для расчета данного интеграла использовался метод Симпсона:
Геометрический
смысл определенного интеграла 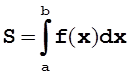 от функции одной
переменной
от функции одной
переменной ![]() - площадь, заключенная под кривой
подынтегральной функции в заданных пределах (рис.4). Его вычисление основано на
разбиении интервала интегрирования
- площадь, заключенная под кривой
подынтегральной функции в заданных пределах (рис.4). Его вычисление основано на
разбиении интервала интегрирования ![]() на ряд элементарных
участков шириной
на ряд элементарных
участков шириной ![]() и последующем представлении
подынтегральной функции на каждом из этих участков какой-либо простой
аппроксимацией. При таком представлении интеграл от каждого элементарного
участка легко вычисляется. Искомый интеграл находится суммированием
элементарных интегралов.
и последующем представлении
подынтегральной функции на каждом из этих участков какой-либо простой
аппроксимацией. При таком представлении интеграл от каждого элементарного
участка легко вычисляется. Искомый интеграл находится суммированием
элементарных интегралов.
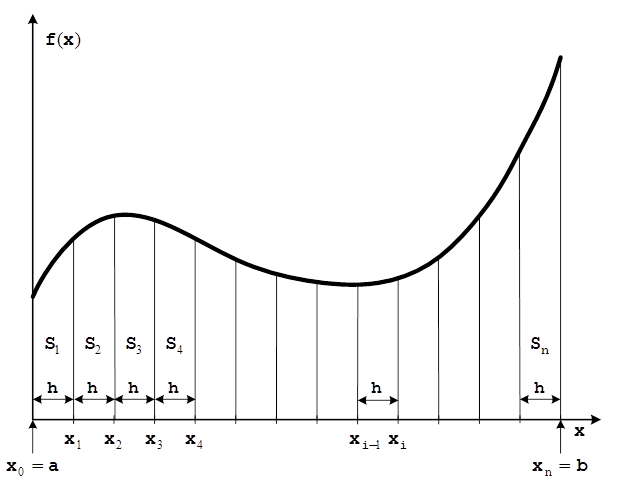
Рис. 3. Разбиение интервала интегрирования на элементарные участки.
Если подынтегральную функцию на двух соседних элементарных участках представить в виде квадратичной параболы, то получим формулу описывающую метод Симпсона:
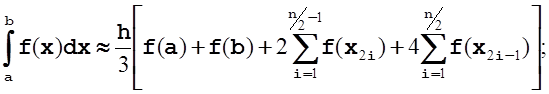 где
где ![]() и
и ![]() -
пределы интегрирования;
-
пределы интегрирования;
![]() - число интервалов интегрирования (
обязательно четное);
- число интервалов интегрирования (
обязательно четное);
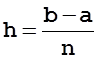 - элементарный интервал (шаг)
интегрирования;
- элементарный интервал (шаг)
интегрирования;
![]() - значения аргумента подынтегральной
функции в
- значения аргумента подынтегральной
функции в ![]() -той точке.
-той точке.
Метод
Симпсона дает достаточно высокую точность. Для монотонных функций при ![]() = 10…20 получается весьма точный
результат. Но если функция на интервале интегрирования немонотонна (синусоида,
функции Бесселя и т.п.), может потребоваться значительно большее число точек.
= 10…20 получается весьма точный
результат. Но если функция на интервале интегрирования немонотонна (синусоида,
функции Бесселя и т.п.), может потребоваться значительно большее число точек.
Для расчета металлургической границы и удельного поверхностного сопротивления использовалась управляющая программа:
#include <conio.h>
#include <iostream.h>
#include <stdio.h>
#include <math.h>
#include "define.h"
#include "datafile.h"
#include "integral.h"
void xj(double Nv,double No,double T,double t, double &xj, double &ros);
//программа для проверки температурной
//зависимости металлургической границы перехода
void main()
{
double t,T,No,Nv,Xj,ROS;
double xj_;
clrscr();
t=7200;
No=5E+19;
Nv=1E+16;
T=1125; //температура [C]
xj(Nv,No,T,t,Xj,ROS);
cout << "Xj = " <<Xj<<" мкм"<< endl;
cout<<"Ros = " << ROS <<" Ом/квадрат "<< endl;
// cout<<"N(0)= "<<N(1E-06)<< endl;
//расчет удельного поверхностного сопротивления
//с помощью решения интеграла методом Симпсона
getch();
}
При температуре T=11250C:
Xj=2.2764 мкм.
ρs=41.4881 Ом/квадрат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.