Статистические методы в физике. Распределение Максвелла: Материалы к лекции по дисциплинам «Физика» и «Концепции современного естествознания»

События разделяют на достоверные, невозможные и случайные (возможные). Достоверному событию отвечает обязательное появление данного признака. Так, при бросании кубика появление любого числа из имеющихся является достоверным событием, которое может наступить и не наступить в данных условиях. Например, выпадение цифры «5» при бросании кубика является случайным событием, так как эта цифра может появиться, а может и не появиться. Количественное предсказание появления случайных событий осуществляется с помощью понятия вероятности.

2. Частотное определение вероятности. Рассмотрим пример с бросанием монеты. Пусть при Nбросаниях N_A раз выпал «орёл». Частотой интересующего нас события (выпадения «орла») называется отношение N_A/N. Вероятностью ω этого события называется предел этого отношения при N→ ∞ .

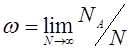(1’)

Формулу (1’) можно применить для определения вероятности нахождения определённой молекулы газа в какой-то части сосуда. В этом случае N – общее число наблюдений, N_A  – число наблюдений, когда молекула находилась в интересующей нас части сосуда.

При решении прикладных задач невозможно провести бесконечное число испытаний, поэтому под вероятностью часто понимают частоту появления данного события при большом числе испытаний (несколько сотен или тысяч).

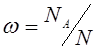      (1)

Определение ω по формуле (1) можно применять во всех случаях, если состояния системы изменяются дискретно (монета в двух состояниях, молекула газа в выбранном объёме или вне его, игральная кость в шести состояниях).

Если провести достаточно большое число испытаний, то вычисление вероятности по формуле (1) не представляет труда. Однако, проведение большого числа испытаний является очень трудоемкой задачей и чаще всего невозможной (например, обнаружение молекулы газа в какой-то части сосуда). Поэтому очень важны теоретические методы нахождения ω.

Наиболее просто можно найти вероятности для, так называемых, равновозможных событий. Равновозможными или равновероятными называются события, частота появления которых одинакова. Заключение о равновероятности событий делается на основе детального анализа свойств системы и характера испытаний. Поясним это на примерах.

Разделим объем, занимаемый идеальным газом, на две равные части. Будем считать, что мы можем различать частицы друг от друга, следить за положением отдельной частицы, не оказывая актом наблюдения существенного влияния на ее движение и состояние наблюдаемой системы в целом. Пусть система находится в неизменных внешних условиях. Найдем вероятность нахождения частицы в одной из половин сосуда. Так как нет никаких физических факторов, которые делали бы для частицы более предпочтительным нахождение в какой-либо одной из половин объема по сравнению с другой, то нахождение в любой половине сосуда является равновероятным. Поэтому при большом числе наблюдений Nв половине случаев частица будет наблюдаться в одной части объёма, а в половине – в другой. Следовательно,  и вероятность обнаружить частицу в одной половине сосуда .

Аналогичные соображения можно применить к бросанию монеты, бросанию кубика. Так как монета, как правило, однородна, то появление «решки» или «орла» одинаково возможно. При одном бросании монеты число возможных случаев равно двум, а число случаев появления «герба