Колебания и волны. Варианты задач по дисциплине “Физика”

Факультет материаловедения

И обработки металлов

давлением                            

Кафедра физики

КОЛЕБАНИЯ И ВОЛНЫ

Варианты задач

по дисциплине “Физика”

Новокузнецк

2003

Министерство образования Российской Федерации

Государственное образовательное учреждение  

    высшего профессионального образования

«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»

КОЛЕБАНИЯ И ВОЛНЫ

Варианты задач

по дисциплине “Физика”

Новокузнецк

2003

УДК 536.7:519.2(07)

К60

Рецензент

Кандидат технических наук

доцент кафедры физики

металлов ГОУ ВПО «СибГИУ»

Н.Н.Кушнаренко

К60 Колебания и волны. Варианты задач по дисциплине “Физика”. /Сост.: Шарафутдинов Р.Ф., Ерилова Т.В.: ГОУ ВПО «СибГИУ».- Новокузнецк, 2003. – 48.

Приводятся задачи для самостоятельного решения в качестве семестровых контрольных заданий (индивидуальных расчетно-графических работ). Задачи разделены по вариантам, снабжены необходимыми рисунками. В ведены основные понятия теории колебаний и волн. Приведены примеры решения задач. Подбор материала ориентирован на курс физики для высших технических учебных заведений.

Работа предназначена для студентов всех специальностей.

Содержание

Стр.

Основные понятия теории колебаний и волн…………………..3

Примеру решения задач…………………………………………11

Варианты задания………………………………………………..17

КОЛЕБАНИЯ И ВОЛНЫ

Основные понятия теории колебаний.

Колебательными процессами (колебаниями) называются изменения состояния систем, обладающие свойством повторяемости во времени. Из всего многообразия колебательных движений рассмотрим прежде такие, в которых изменяющаяся физическая величина описывается в зависимости от времени  законом синуса или косинуса.

Анализируя различные по своей природе колебания, такие как колебания груза, на пружине, математического маятника, процессы изменения во времени некоторых величин в колебательном контуре, в отсутствии сил сопротивления, можно придти к выводу, что все упомянутые колебания имеют общие закономерности и описываются  одними и теми же математическими методами.

Гармонические колебания представляют собой частный случай периодических колебаний, при которых значения физических величин  изменяющихся в процессе колебаний, повторяются через одинаковые промежутки времени.

Уравнение гармонических колебаний имеет следующий вид:

,   (или ),    (1)

где x- смещение колеблющейся точки из положения равновесия,

А - амплитуда - максимальное смещение колеблющейся величины из положения равновесия (когда значения   функций  косинуса либо синуса принимают максимальные значения равные единице),

- циклическая частота колебаний,

(+) - фаза колебания, показывает какая часть периода прошла с момента начала колебаний, и определяет значение изменяющейся величины в данный момент времени.

- начальная фаза колебания, определяющая смещение точки из положения равновесия в начальный момент времени равный 0.

Время, в течение которого совершается одно полное колебание, называется периодом колебаний Т

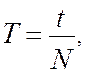                                     (2)

где N - число полных колебаний за время t. Величина обратная периоду колебаний называется частотой колебаний и измеряется в Герцах (Гц) или в с^-1.

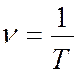                                        (3).

Циклической частотой  называется число полных колебаний, совершаемых  в течении 2 секунд

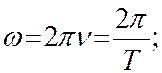                           (4)

 измеряется в с^-1.

                        1.  Собственные колебания.

Если на систему, совершающую колебания, не влияют внешние воздействия то ее колебания называются свободными или собственными. В  этом случае не происходит рассеивание энергии в окружающее пространство (в виде работы против сил сопротивления) и такие колебания  называются незатухающими. Они характеризуются строгой периодичностью.

Кинематика колебательного движения задается уравнениями:

1. Проекцией скорости 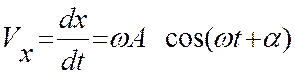              (5)

где  =V_max - амплитудное значение скорости.

2.Проекция ускорения при гармонических колебаниях:

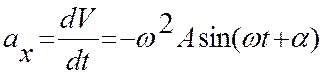       (6)

где 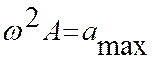- амплитудное значение ускорения.

Таким образом, и скорость и ускорение являются периодическими функциями времени той же самой частоты, что и смещение x.

Скорость и ускорение сдвинуты по фазе относительно смещения соответственно на /2 и на .

Динамика материальной точки при колебательном движении определяется вторым законом Ньютона:

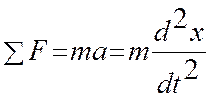,                       (7)

который надо записать для конкретной задачи, учтя все силы, действующие на колеблющуюся точку. В случае гармонических колебаний обычно представляет собой единственную упругую (или квазиупругую) силу, направленную к положению равновесия:

для маятника на пружине - это  cила упругости,

                                             F=-kx                                (8)                                                                         здесь к -коэффициент упругости (или жесткости). При подстановки (8) в уравнение (7), получается однородное дифференциальное уравнение второго порядка без правой части:

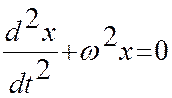                           (9).

Решением этого дифференциального уравнения являются уравнения типа (1), что легко проверяется подстановкой. В уравнение (9) величину ² =принято обозначать через 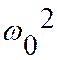, а  называть частотой собственныхколебаний. Поэтому уравнение (9) следует записать так:

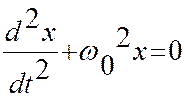                               (10).              

Частота  связана с периодом собственных колебаний (4) и позволяет его вычислять. Так для частных случаев период равен

Т =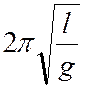      для математического маятника с длиной подвеса l;

Т = 2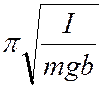 для физического маятника. Здесь I- момент инерции тела относительно точки подвеса, b- расстояние от точки подвеса до центра массы маятника.

T = 2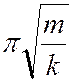    для пружинного маятника (k- жесткость пружины);

Т = 2   для колебательного контура (L и C - индуктивность катушки и емкость конденсатора соответственно).

Кинетическая и потенциальная энергии  колеблющейся точки имеют следующий вид:

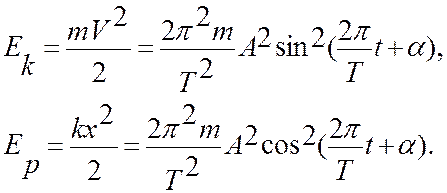     (11)

Полная энергия в любой момент времени равна сумме кинетической и потенциальной энергий:

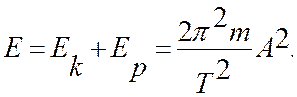                (12)

Из (11), в частности,  следует, что частота изменений кинетической и потенциальной энергии колеблющейся физической величины в два раза больше частоты собственных колебаний.

Колеблющаяся точка может участвовать одновременно в нескольких колебательных движениях. Такие колебания складываются.

В случае сложения колебаний одинакового направления и одинаковой частоты получается гармоническое колебание того же периода с амплитудой

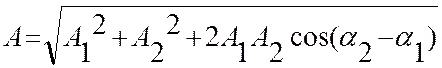      (13)

и с начальной фазой, которая определяется из уравнения

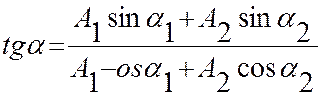                      (14)

где А₁ и А₂- амплитуды складываемых колебаний, а  и  их начальные фазы.

В случае сложения двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории имеет вид эллипса